DNN网络（一）

摘自

https://www.cnblogs.com/pinard/p/6418668.html

一、DNN 简介

1.DNN的层次可以分为三层

• 输入层（input layer）
• 隐藏层（hidden layer）
• 输出层（output layer）

2.连接关系

• 设每一层的权重参数为ωⁱ_ab。i代表第几层，a代表i层下第a个神经元的权重, b代表第i层下第a个神经元到i+1层第b个神经元的偏置量。zⁱ _a代表i层第a个神经元的线性变换输入值。σⁱ_a(zⁱ_a)代表i层第a个神经元通过激励函数的输入值。
  
• 其中第i层，b个神经元的线性输入为zⁱ _b= Σx^i-1_ab*ω^i-1_ab + bⁱ_b. 如果非第一层，xⁱ_ab= σⁱ_a(zⁱ_a)，否则为本身。σ(z)为激活函数的变换，这也是从上一层到下一层是通过什么激活函数转换的。
• 上图所示的网络是全连接的，即i-1层的神经元与i层的任意神经元连接。

二、DNN的前向传播

1.正如上一节中连接关系介绍的，通过线性变换，第i层的输入可以从第i-1层的输出得到，这也是前向传播算法。

2.由上一节的分析，可以得到第i层，第a个神经元yⁱ_a的输出：

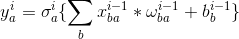
3.例如，假设第一层有三个神经元，第2层的第1、2、3个神经元的输出为：

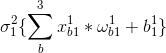
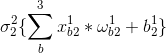
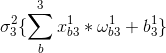
4.用矩阵表示计算过程2更加简洁：

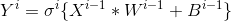
三、小结

以上为DNN的前向传播算法，其实就是从头向后一直计算。先从输入层计算，然后计算各个隐藏层的神经元的值。最后通过隐藏层得到输出层的值。前向传播就是计算一层接着一层的输出。但是，每一层的参数是需要优化的，而优化的过程又称为反向传播算法。