Gym - 101848C Object-Oriented Programming （树链剖分+线段树+动态开点）

C. Object-Oriented Programming

time limit per test

3.0 s

memory limit per test

1024 MB

input

standard input

output

standard output

Functions overriding, is a well-known concept, when we are using inheritance in Object-Oriented Programming (OOP). For those who are not familiar with OOP, I will recall a few things to perhaps refresh your memory.

• A class has at most one parent class. When they do, they are called subclasses inheriting their parents. Subclasses also inherit all the functions declared in their parent classes, and also, all the functions inherited by parents' parents, and so on. Here, we refer to the ancestors as superclasses.
• Subclasses can, of course, declare new functions, and also override the functions already declared in superclasses. This is called overriding.
• When an instance of the subclass calls a function, it will first try to find the code in its own class body, and then its parent, and then its parent's parent, etc., until it reaches the root (the superclass of all classes). If the function has still not been found yet, a runtime error will be raised.

As you might have guessed, we are interested in finding out in which class the function is written when some instance of a particular class calls it.

Input

The input is in the following format:

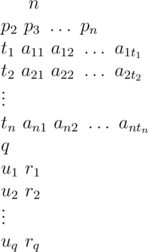
n (2 ≤ n ≤ 105) is the number of classes. Classes are numbered from 1 to n. pi (1 ≤ pi ≤ i - 1) is the parent class of class i. Class 1 is the root class, superclass of all classes. It has no parent.

ti denotes the number of functions written in class i, including both new functions and overriding functions. Then follows ai1, ai2, ..., aiti a list of these functions. Functions are also denoted using positive integers. It's guaranteed that every number will appear at most once in one list. 1 ≤ aij ≤ 106, 0 ≤ ti ≤ 106, .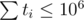

q (1 ≤ q ≤ 105) is the query number. Then follows q queries. ui, ri (1 ≤ ui ≤ n, 1 ≤ ri ≤ 106) is the i-th query, asking when an instance of class ui calls function ri, in which class is this function written?

Output

For each query, print answer. If it is illegal, that is, a "runtime error" is raised, then output  - 1.

Example

input

Copy

5
1 2 3 3
2 2 1
0
2 5 2
2 4 5
1 5
4
3 4
5 2
4 5
1 3

output

Copy

-1
3
4
-1

Note

The sample is equivalent to the following Java code.

class Class1 {
    void function2() { System.out.println("1"); }
    void function1() { System.out.println("1"); }
}

class Class2 extends Class1 {

}

class Class3 extends Class2 {
    void function5() { System.out.println("3"); }
    void function2() { System.out.println("3"); }
}

class Class4 extends Class3 {
    void function4() { System.out.println("4"); }
    void function5() { System.out.println("4"); }
}

class Class5 extends Class3 {
    void function5() { System.out.println("5"); }
}

void test() {
    new Class3().function4();
    new Class5().function2();
    new Class4().function5();
    new Class1().function3();
}

Some of the tests in the raw problem package have been removed due to the "Maximal summary testset file size exceeded" error on Codeforces.

题意：

题面说的很复杂，但是我们可以将他转换成一个比较直白的模型：

给你n个点，依此输入n-1条边，形成一棵树。然后依此输入n行，依此表示1-n这几个点每个点含有哪几个值（一个点可以包含多个值，也可以不包含值，如果一条路径上，后面的点包含的值如果和前面点包含的值相同，在询问时会覆盖前面的），然后q个询问，每个询问输入两个值：u,r;询问u到根节点路径上哪个点包含r这个值（相同的值后面点覆盖前面点），输出这个点的坐标。

思路：

我们对每个值建一棵树，将包含这些值的点存进树里，点i就将树上点i标为i，然后询问u,r时,我们只要询问第r棵树上1-u上最大值就好了（用个链剖+线段树就好了），建树的话直接动态开点就行了不会超内存，这样的话这道题就很好写了。。

如果想到了思路就很好写，之前想歪了思路，debug了半天都没有得到想要的值。

实现代码：

#include<bits/stdc++.h>
using namespace std;
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
const int Max = 3e7+;
const int M = 2e6+;
const int MM = 2e6;
int ls[Max],rs[Max],sum[Max],root[Max],idx,ed[Max];
struct node{
    int to,next;
}e[M];
int cnt,cnt1,n;
int son[M],siz[M],head[M],fa[M],top[M],dep[M],tid[M],mx[M],rk[M];
void add(int u,int v){
    e[++cnt].to = v;e[cnt].next = head[u];head[u] = cnt;
}

void dfs1(int u,int faz,int deep){
    dep[u] = deep;
    fa[u] = faz;
    siz[u] = ;
    for(int i = head[u];i;i = e[i].next){
        int v = e[i].to;
        if(v == faz) continue;
        dfs1(v,u,deep+);
        siz[u] += siz[v];
        if(siz[v] > siz[son[u]]||son[u] == -)
            son[u] = v;
    }
}

void dfs2(int u,int t){
    top[u] = t;
    mx[u] = cnt1;
    tid[u] = cnt1;
    rk[cnt1] = u;
    cnt1++;
    if(son[u] == -) return ;
    dfs2(son[u],t),mx[u] = max(mx[u],mx[son[u]]);
    for(int i = head[u];i;i=e[i].next){
        int v = e[i].to;
        if(v != fa[u]&&v != son[u])
            dfs2(v,v),mx[u] = max(mx[u],mx[v]);
    }
}

void update(int &k,int l,int r,int p,int num){
    if(!k){
        k = ++idx;
        sum[k] = num;
    }
    sum[k] = max(sum[k],num);
    if(l == r)
        return ;
    int m = (l + r) >> ;
    if(p <= m) update(ls[k],l,m,p,num);
    else update(rs[k],m+,r,p,num);
}

int query(int k,int L,int R,int l,int r){
    if(!k) return ;
    if(L <= l&&R >= r){
        return sum[k];
    }
    int m = (l + r) >> ;
    int ans = ;
    if(L <= m) ans = max(ans,query(ls[k],L,R,l,m));
    if(R > m) ans = max(ans,query(rs[k],L,R,m+,r));
    return ans;
}

int solve(int x,int y,int rt){
    int fx = top[x],fy = top[y];
    int ans = ;
    while(fx != fy){
        if(dep[fx] < dep[fy]) swap(x,y),swap(fx,fy);
        ans = max(ans,query(root[rt],tid[fx],tid[x],,MM));
        x = fa[fx]; fx = top[x];
    }
    if(dep[x] > dep[y]) swap(x,y);
    ans = max(ans,query(root[rt],tid[x],tid[y],,MM));
    return ans;
}

int main()
{
    int x,k,q,t,n;
    idx = ;
    cnt1 = ; cnt = ;
    root[] = ,sum[] = ;
    scanf("%d",&n);
    memset(son,-,sizeof(son));
    for(int i = ;i <= n;i ++){
        scanf("%d",&x);
        add(x,i); add(i,x);
    }
    dfs1(,,); dfs2(,);
    for(int i = ;i <= n;i ++){
        scanf("%d",&t);
        for(int j = ;j <= t;j ++){
            scanf("%d",&x);
            update(root[x],,MM,tid[i],i);
        }
    }
    scanf("%d",&q);
    while(q--){
        scanf("%d %d",&k,&x);
        //cout<<"kk: "<<k<<" "<<root[k]<<endl;
        int num = solve(,k,x);
        if(num == ) num = -;
        printf("%d\n",num);
    }
    return ;
}