吴恩达课后作业学习1-week4-homework-multi-hidden-layer -2

参考：https://blog.csdn.net/u013733326/article/details/79767169

希望大家直接到上面的网址去查看代码，下面是本人的笔记

实现多层神经网络

1.准备软件包

import numpy as np
import h5py
import matplotlib.pyplot as plt
import testCases #参见资料包，或者在文章底部copy
from dnn_utils import sigmoid, sigmoid_backward, relu, relu_backward #参见资料包
import lr_utils #参见资料包，或者在文章底部copy

为了和作者的数据匹配，需要指定随机种子

np.random.seed(1)

2.初始化参数

def initialize_parameters_deep(layers_dims):
    """
    此函数是为了初始化多层网络参数而使用的函数。
    参数：
        layers_dims - 包含我们网络中每个图层的节点数量的列表

    返回：
        parameters - 包含参数“W1”，“b1”，...，“WL”，“bL”的字典：
                     W1 - 权重矩阵，维度为（layers_dims []，layers_dims [-]）
                     bl - 偏向量，维度为（layers_dims []，）
    """
    np.random.seed()
    parameters = {}
    L = len(layers_dims)

    for l in range(,L):
        parameters["W" + str(l)] = np.random.randn(layers_dims[l], layers_dims[l - ]) / np.sqrt(layers_dims[l - ])
        parameters["b" + str(l)] = np.zeros((layers_dims[l], ))

        #确保我要的数据的格式是正确的
        assert(parameters["W" + str(l)].shape == (layers_dims[l], layers_dims[l-]))
        assert(parameters["b" + str(l)].shape == (layers_dims[l], ))

    return parameters

测试两层时：

#测试initialize_parameters_deep
print("==============测试initialize_parameters_deep==============")
layers_dims = [,,] #这个其实也是实现了两层
parameters = initialize_parameters_deep(layers_dims)
print(parameters)
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))

返回：

==============测试initialize_parameters_deep==============
{'W1': array([[ 0.79989897,  0.19521314,  0.04315498, -0.83337927, -0.12405178],
       [-0.15865304, -0.03700312, -0.28040323, -0.01959608, -0.21341839],
       [-0.58757818,  0.39561516,  0.39413741,  0.76454432,  0.02237573],
       [-0.18097724, -0.24389238, -0.69160568,  0.43932807, -0.49241241]]), 'b1': array([[.],
       [.],
       [.],
       [.]]), 'W2': array([[-0.59252326, -0.10282495,  0.74307418,  0.11835813],
       [-0.51189257, -0.3564966 ,  0.31262248, -0.08025668],
       [-0.38441818, -0.11501536,  0.37252813,  0.98805539]]), 'b2': array([[.],
       [.],
       [.]])}
W1 = [[ 0.79989897  0.19521314  0.04315498 -0.83337927 -0.12405178]
 [-0.15865304 -0.03700312 -0.28040323 -0.01959608 -0.21341839]
 [-0.58757818  0.39561516  0.39413741  0.76454432  0.02237573]
 [-0.18097724 -0.24389238 -0.69160568  0.43932807 -0.49241241]]
b1 = [[.]
 [.]
 [.]
 [.]]
W2 = [[-0.59252326 -0.10282495  0.74307418  0.11835813]
 [-0.51189257 -0.3564966   0.31262248 -0.08025668]
 [-0.38441818 -0.11501536  0.37252813  0.98805539]]
b2 = [[.]
 [.]
 [.]]

测试三层时：

#测试initialize_parameters_deep
print("==============测试initialize_parameters_deep==============")
layers_dims = [,,,] #实现三层看看
parameters = initialize_parameters_deep(layers_dims)
print(parameters)
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
print("W3 = " + str(parameters["W3"]))
print("b3 = " + str(parameters["b3"]))

返回：

==============测试initialize_parameters_deep==============
{'W1': array([[ 0.79989897,  0.19521314,  0.04315498, -0.83337927, -0.12405178],
       [-0.15865304, -0.03700312, -0.28040323, -0.01959608, -0.21341839],
       [-0.58757818,  0.39561516,  0.39413741,  0.76454432,  0.02237573],
       [-0.18097724, -0.24389238, -0.69160568,  0.43932807, -0.49241241]]), 'b1': array([[.],
       [.],
       [.],
       [.]]), 'W2': array([[-0.59252326, -0.10282495,  0.74307418,  0.11835813],
       [-0.51189257, -0.3564966 ,  0.31262248, -0.08025668],
       [-0.38441818, -0.11501536,  0.37252813,  0.98805539]]), 'b2': array([[.],
       [.],
       [.]]), 'W3': array([[-0.71829494, -0.36166197, -0.46405457],
       [-1.39665832, -0.53335157, -0.59113495]]), 'b3': array([[.],
       [.]])}
W1 = [[ 0.79989897  0.19521314  0.04315498 -0.83337927 -0.12405178]
 [-0.15865304 -0.03700312 -0.28040323 -0.01959608 -0.21341839]
 [-0.58757818  0.39561516  0.39413741  0.76454432  0.02237573]
 [-0.18097724 -0.24389238 -0.69160568  0.43932807 -0.49241241]]
b1 = [[.]
 [.]
 [.]
 [.]]
W2 = [[-0.59252326 -0.10282495  0.74307418  0.11835813]
 [-0.51189257 -0.3564966   0.31262248 -0.08025668]
 [-0.38441818 -0.11501536  0.37252813  0.98805539]]
b2 = [[.]
 [.]
 [.]]
W3 = [[-0.71829494 -0.36166197 -0.46405457]
 [-1.39665832 -0.53335157 -0.59113495]]
b3 = [[.]
 [.]]

3）前向传播

def L_model_forward(X,parameters):
    """
    实现[LINEAR-> RELU] *（L-） - > LINEAR-> SIGMOID计算前向传播，也就是多层网络的前向传播，为后面每一层都执行LINEAR和ACTIVATION

    参数：
        X - 数据，numpy数组，维度为（输入节点数量，示例数）
        parameters - initialize_parameters_deep（）的输出

    返回：
        AL - 最后的激活值
        caches - 包含以下内容的缓存列表：
                 linear_relu_forward（）的每个cache（有L-1个，索引为从0到L-）
                 linear_sigmoid_forward（）的cache（只有一个，索引为L-）
    """
    caches = []
    A = X
    L = len(parameters) //
    for l in range(,L):
        A_prev = A
        A, cache = linear_activation_forward(A_prev, parameters['W' + str(l)], parameters['b' + str(l)], "relu")
        caches.append(cache)

    #最后一层使用sigmoid函数进行二分类
    AL, cache = linear_activation_forward(A, parameters['W' + str(L)], parameters['b' + str(L)], "sigmoid")
    caches.append(cache)

    assert(AL.shape == (,X.shape[]))

    return AL,caches

上面函数使用的线性激活函数linear_activation_forward：

def linear_activation_forward(A_prev,W,b,activation):
    """
    实现LINEAR-> ACTIVATION 这一层的前向传播

    参数：
        A_prev - 来自上一层（或输入层）的激活，维度为(上一层的节点数量，示例数）
        W - 权重矩阵，numpy数组，维度为（当前层的节点数量，前一层的大小）
        b - 偏向量，numpy阵列，维度为（当前层的节点数量，）
        activation - 选择在此层中使用的激活函数名，字符串类型，【"sigmoid" | "relu"】

    返回：
        A - 激活函数的输出，也称为激活后的值
        cache - 一个包含“linear_cache”和“activation_cache”的字典，我们需要存储它以有效地计算后向传递
    """

    if activation == "sigmoid":
        Z, linear_cache = linear_forward(A_prev, W, b)
        A, activation_cache = sigmoid(Z)
    elif activation == "relu":
        Z, linear_cache = linear_forward(A_prev, W, b)
        A, activation_cache = relu(Z)

    assert(A.shape == (W.shape[],A_prev.shape[]))
    cache = (linear_cache,activation_cache)

    return A,cache

测试函数L_model_forward_test_case()：

def L_model_forward_test_case(): #两层
    """
    X = np.array([[-1.02387576, 1.12397796],
 [-1.62328545, 0.64667545],
 [-1.74314104, -0.59664964]])
    parameters = {'W1': np.array([[ 1.62434536, -0.61175641, -0.52817175],
        [-1.07296862,  0.86540763, -2.3015387 ]]),
 'W2': np.array([[ 1.74481176, -0.7612069 ]]),
 'b1': np.array([[ .],
        [ .]]),
 'b2': np.array([[ .]])}
    """
    np.random.seed()
    X = np.random.randn(,)
    W1 = np.random.randn(,)
    b1 = np.random.randn(,)
    W2 = np.random.randn(,)
    b2 = np.random.randn(,)
    parameters = {"W1": W1,
                  "b1": b1,
                  "W2": W2,
                  "b2": b2}

    return X, parameters

测试：

#测试L_model_forward
print("==============测试L_model_forward==============")
X,parameters = testCases.L_model_forward_test_case()
print(parameters)
AL,caches = L_model_forward(X,parameters)
print("AL = " + str(AL))
print("caches 的长度为 = " + str(len(caches)))
print(caches)

返回：

==============测试L_model_forward==============
{'W1': array([[ 0.3190391 , -0.24937038,  1.46210794, -2.06014071],
       [-0.3224172 , -0.38405435,  1.13376944, -1.09989127],
       [-0.17242821, -0.87785842,  0.04221375,  0.58281521]]), 'b1': array([[-1.10061918],
       [ 1.14472371],
       [ 0.90159072]]), 'W2': array([[ 0.50249434,  0.90085595, -0.68372786]]), 'b2': array([[-0.12289023]])}
AL = [[0.17007265 0.2524272 ]]
caches 的长度为 =
[((array([[ 1.62434536, -0.61175641],
       [-0.52817175, -1.07296862],
       [ 0.86540763, -2.3015387 ],
       [ 1.74481176, -0.7612069 ]]), array([[ 0.3190391 , -0.24937038,  1.46210794, -2.06014071],
       [-0.3224172 , -0.38405435,  1.13376944, -1.09989127],
       [-0.17242821, -0.87785842,  0.04221375,  0.58281521]]), array([[-1.10061918],
       [ 1.14472371],
       [ 0.90159072]])), array([[-2.77991749, -2.82513147],
       [-0.11407702, -0.01812665],
       [ 2.13860272,  1.40818979]])), ((array([[.        , .        ],
       [.        , .        ],
       [2.13860272, 1.40818979]]), array([[ 0.50249434,  0.90085595, -0.68372786]]), array([[-0.12289023]])), array([[-1.58511248, -1.08570881]]))]

4.计算成本

def compute_cost(AL,Y):
    """
    实施等式（4）定义的成本函数。

    参数：
        AL - 与标签预测相对应的概率向量，维度为（1，示例数量）
        Y - 标签向量（例如：如果不是猫，则为0，如果是猫则为1），维度为（1，数量）

    返回：
        cost - 交叉熵成本
    """
    m = Y.shape[1]
    cost = -np.sum(np.multiply(np.log(AL),Y) + np.multiply(np.log(1 - AL), 1 - Y)) / m

    cost = np.squeeze(cost)
    assert(cost.shape == ())

    return cost

测试函数：

def compute_cost_test_case():
    Y = np.asarray([[1, 1, 1]])
    aL = np.array([[.8,.9,0.4]])

    return Y, aL

测试：

#测试compute_cost
print("==============测试compute_cost==============")
Y,AL = testCases.compute_cost_test_case()
print("cost = " + str(compute_cost(AL, Y)))

返回：

==============测试compute_cost==============
cost = 0.414931599615397

5.后向传播

因为最后的输出层使用的是sigmoid函数，隐藏层使用的是Relu函数

所以需要对最后一层进行特殊计算，其他层迭代即可

即A^[L]，它属于输出层的输出，A^[L]=σ(Z^[L])，所以我们需要计算dA^L，我们可以使用下面的代码来计算它：

dAL = - (np.divide(Y, AL) - np.divide( - Y,  - AL))

计算完了以后，我们可以使用此激活后的梯度dA^L继续向后计算

其实是先通过线性激活部分后向传播得到dz，然后再将dz带入线性部分的后向传播得到dw,db,dA_prev

1）线性部分

根据这三个公式来构建后向传播函数

def linear_backward(dZ,cache):
    """
    为单层实现反向传播的线性部分（第L层）

    参数：
         dZ - 相对于（当前第l层的）线性输出的成本梯度
         cache - 来自当前层前向传播的值的元组（A_prev，W，b）

    返回：
         dA_prev - 相对于激活（前一层l-1）的成本梯度，与A_prev维度相同
         dW - 相对于W（当前层l）的成本梯度，与W的维度相同
         db - 相对于b（当前层l）的成本梯度，与b维度相同
    """
    A_prev, W, b = cache
    m = A_prev.shape[1]
    dW = np.dot(dZ, A_prev.T) / m
    db = np.sum(dZ, axis=1, keepdims=True) / m
    dA_prev = np.dot(W.T, dZ)

    assert (dA_prev.shape == A_prev.shape)
    assert (dW.shape == W.shape)
    assert (db.shape == b.shape)

    return dA_prev, dW, db

2）线性激活部分

将线性部分也使用了进来

在dnn_utils.py中定义了两个现成可用的后向函数，用来帮助计算dz：

如果 g(.)是激活函数, 那么sigmoid_backward 和 relu_backward 这样计算：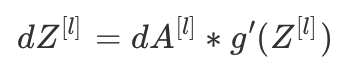

• sigmoid_backward:实现了sigmoid（）函数的反向传播，用来计算dz为：

dZ = sigmoid_backward(dA, activation_cache)

• relu_backward: 实现了relu（）函数的反向传播，用来计算dz为：

dZ = relu_backward(dA, activation_cache)

后向函数为：

def sigmoid_backward(dA, cache):
    """
    Implement the backward propagation for a single SIGMOID unit.

    Arguments:
    dA -- post-activation gradient, of any shape
    cache -- 'Z' where we store for computing backward propagation efficiently

    Returns:
    dZ -- Gradient of the cost with respect to Z
    """

    Z = cache

    s = 1/(1+np.exp(-Z))
    dZ = dA * s * (1-s)

    assert (dZ.shape == Z.shape)

    return dZ

def relu_backward(dA, cache):
    """
    Implement the backward propagation for a single RELU unit.

    Arguments:
    dA -- post-activation gradient, of any shape
    cache -- 'Z' where we store for computing backward propagation efficiently

    Returns:
    dZ -- Gradient of the cost with respect to Z
    """

    Z = cache
    dZ = np.array(dA, copy=True) # just converting dz to a correct object.

    # When z <= 0, you should set dz to 0 as well.
    dZ[Z <= 0] = 0

    assert (dZ.shape == Z.shape)

    return dZ

代码为：

def linear_activation_backward(dA,cache,activation="relu"):
    """
    实现LINEAR-> ACTIVATION层的后向传播。

    参数：
         dA - 当前层l的激活后的梯度值
         cache - 我们存储的用于有效计算反向传播的值的元组（值为linear_cache，activation_cache）
         activation - 要在此层中使用的激活函数名，字符串类型，【"sigmoid" | "relu"】
    返回：
         dA_prev - 相对于激活（前一层l-1）的成本梯度值，与A_prev维度相同
         dW - 相对于W（当前层l）的成本梯度值，与W的维度相同
         db - 相对于b（当前层l）的成本梯度值，与b的维度相同
    """
    linear_cache, activation_cache = cache
    #其实是先通过线性激活部分后向传播得到dz，然后再将dz带入线性部分的后向传播得到dw,db,dA_prev
    if activation == "relu":
        dZ = relu_backward(dA, activation_cache)
        dA_prev, dW, db = linear_backward(dZ, linear_cache)
    elif activation == "sigmoid":
        dZ = sigmoid_backward(dA, activation_cache)
        dA_prev, dW, db = linear_backward(dZ, linear_cache)

    return dA_prev,dW,db

整合函数，用于多层神经网络：

def L_model_backward(AL,Y,caches):
    """
    对[LINEAR-> RELU] *（L-） - > LINEAR - > SIGMOID组执行反向传播，就是多层网络的向后传播

    参数：
     AL - 概率向量，正向传播输出层的输出（L_model_forward（））
     Y - 标签向量，真正正确的结果（例如：如果不是猫，则为0，如果是猫则为1），维度为（，数量）
     caches - 包含以下内容的cache列表：
                 linear_activation_forward（"relu"）的cache，不包含输出层
                 linear_activation_forward（"sigmoid"）的cache

    返回：
     grads - 具有梯度值的字典
              grads [“dA”+ str（l）] = ...
              grads [“dW”+ str（l）] = ...
              grads [“db”+ str（l）] = ...
    """
    grads = {}
    L = len(caches)
    m = AL.shape[] #得到数据量，几张照片
    Y = Y.reshape(AL.shape) #保证AL和Y两者格式相同
    dAL = - (np.divide(Y, AL) - np.divide( - Y,  - AL)) #计算得到dAL

    current_cache = caches[L-] #用于输出层的cache存储的值
    #对输出层进行后向传播
    grads["dA" + str(L)], grads["dW" + str(L)], grads["db" + str(L)] = linear_activation_backward(dAL, current_cache, "sigmoid")

    for l in reversed(range(L-)): #迭代对接下来的隐藏层进行后向传播
        current_cache = caches[l]
        dA_prev_temp, dW_temp, db_temp = linear_activation_backward(grads["dA" + str(l + )], current_cache, "relu")
        grads["dA" + str(l + )] = dA_prev_temp
        grads["dW" + str(l + )] = dW_temp
        grads["db" + str(l + )] = db_temp

    return grads

测试函数：

def L_model_backward_test_case(): #计算后向传播的前向传播的值
    """
    X = np.random.rand(,)
    Y = np.array([[, ]])
    parameters = {'W1': np.array([[ 1.78862847,  0.43650985,  0.09649747]]), 'b1': np.array([[ .]])}

    aL, caches = (np.array([[ 0.60298372,  0.87182628]]), [((np.array([[ 0.20445225,  0.87811744],
           [ 0.02738759,  0.67046751],
           [ 0.4173048 ,  0.55868983]]),
    np.array([[ 1.78862847,  0.43650985,  0.09649747]]),
    np.array([[ .]])),
   np.array([[ 0.41791293,  1.91720367]]))])
   """
    np.random.seed()
    AL = np.random.randn(, )
    Y = np.array([[, ]])

    A1 = np.random.randn(,)
    W1 = np.random.randn(,)
    b1 = np.random.randn(,)
    Z1 = np.random.randn(,)
    linear_cache_activation_1 = ((A1, W1, b1), Z1)

    A2 = np.random.randn(,)
    W2 = np.random.randn(,)
    b2 = np.random.randn(,)
    Z2 = np.random.randn(,)
    linear_cache_activation_2 = ( (A2, W2, b2), Z2)

    caches = (linear_cache_activation_1, linear_cache_activation_2)

    return AL, Y, caches

测试：

#测试L_model_backward
print("==============测试L_model_backward==============")
AL, Y_assess, caches = testCases.L_model_backward_test_case()
grads = L_model_backward(AL, Y_assess, caches)
print ("dW1 = "+ str(grads["dW1"]))
print ("db1 = "+ str(grads["db1"]))
print ("dA1 = "+ str(grads["dA1"]))

返回：

==============测试L_model_backward==============
dW1 = [[0.41010002 0.07807203 0.13798444 0.10502167]
 [.         .         .         .        ]
 [0.05283652 0.01005865 0.01777766 0.0135308 ]]
db1 = [[-0.22007063]
 [ .        ]
 [-0.02835349]]
dA1 = [[ .          0.52257901]
 [ .         -0.3269206 ]
 [ .         -0.32070404]
 [ .         -0.74079187]]

6.更新参数

根据上面后向传播得到的dw,db,dA_prev来更新参数，其中 α 是学习率

函数：

def update_parameters(parameters, grads, learning_rate):
    """
    使用梯度下降更新参数

    参数：
     parameters - 包含你的参数的字典，即w和b
     grads - 包含梯度值的字典，是L_model_backward的输出

    返回：
     parameters - 包含更新参数的字典
                   参数[“W”+ str（l）] = ...
                   参数[“b”+ str（l）] = ...
    """
    L = len(parameters) // 2 #整除2，得到层数
    for l in range(L):
        parameters["W" + str(l + 1)] = parameters["W" + str(l + 1)] - learning_rate * grads["dW" + str(l + 1)]
        parameters["b" + str(l + 1)] = parameters["b" + str(l + 1)] - learning_rate * grads["db" + str(l + 1)]

    return parameters

测试函数：

def update_parameters_test_case():
    """
    parameters = {'W1': np.array([[ 1.78862847,  0.43650985,  0.09649747],
        [-1.8634927 , -0.2773882 , -0.35475898],
        [-0.08274148, -0.62700068, -0.04381817],
        [-0.47721803, -1.31386475,  0.88462238]]),
 'W2': np.array([[ 0.88131804,  1.70957306,  0.05003364, -0.40467741],
        [-0.54535995, -1.54647732,  0.98236743, -1.10106763],
        [-1.18504653, -0.2056499 ,  1.48614836,  0.23671627]]),
 'W3': np.array([[-1.02378514, -0.7129932 ,  0.62524497],
        [-0.16051336, -0.76883635, -0.23003072]]),
 'b1': np.array([[ 0.],
        [ 0.],
        [ 0.],
        [ 0.]]),
 'b2': np.array([[ 0.],
        [ 0.],
        [ 0.]]),
 'b3': np.array([[ 0.],
        [ 0.]])}
    grads = {'dW1': np.array([[ 0.63070583,  0.66482653,  0.18308507],
        [ 0.        ,  0.        ,  0.        ],
        [ 0.        ,  0.        ,  0.        ],
        [ 0.        ,  0.        ,  0.        ]]),
 'dW2': np.array([[ 1.62934255,  0.        ,  0.        ,  0.        ],
        [ 0.        ,  0.        ,  0.        ,  0.        ],
        [ 0.        ,  0.        ,  0.        ,  0.        ]]),
 'dW3': np.array([[-1.40260776,  0.        ,  0.        ]]),
 'da1': np.array([[ 0.70760786,  0.65063504],
        [ 0.17268975,  0.15878569],
        [ 0.03817582,  0.03510211]]),
 'da2': np.array([[ 0.39561478,  0.36376198],
        [ 0.7674101 ,  0.70562233],
        [ 0.0224596 ,  0.02065127],
        [-0.18165561, -0.16702967]]),
 'da3': np.array([[ 0.44888991,  0.41274769],
        [ 0.31261975,  0.28744927],
        [-0.27414557, -0.25207283]]),
 'db1': 0.75937676204411464,
 'db2': 0.86163759922811056,
 'db3': -0.84161956022334572}
    """
    np.random.seed(2)
    W1 = np.random.randn(3,4)
    b1 = np.random.randn(3,1)
    W2 = np.random.randn(1,3)
    b2 = np.random.randn(1,1)
    parameters = {"W1": W1,
                  "b1": b1,
                  "W2": W2,
                  "b2": b2}
    np.random.seed(3)
    dW1 = np.random.randn(3,4)
    db1 = np.random.randn(3,1)
    dW2 = np.random.randn(1,3)
    db2 = np.random.randn(1,1)
    grads = {"dW1": dW1,
             "db1": db1,
             "dW2": dW2,
             "db2": db2}

    return parameters, grads

测试：

#测试update_parameters
print("==============测试update_parameters==============")
parameters, grads = testCases.update_parameters_test_case()
parameters = update_parameters(parameters, grads, 0.1)

print ("W1 = "+ str(parameters["W1"]))
print ("b1 = "+ str(parameters["b1"]))
print ("W2 = "+ str(parameters["W2"]))
print ("b2 = "+ str(parameters["b2"]))

返回：

==============测试update_parameters==============
W1 = [[-0.59562069 -0.09991781 -2.14584584  1.82662008]
 [-1.76569676 -0.80627147  0.51115557 -1.18258802]
 [-1.0535704  -0.86128581  0.68284052  2.20374577]]
b1 = [[-0.04659241]
 [-1.28888275]
 [ 0.53405496]]
W2 = [[-0.55569196  0.0354055   1.32964895]]
b2 = [[-0.84610769]]

7.整合函数——训练

def L_layer_model(X, Y, layers_dims, learning_rate=0.0075, num_iterations=, print_cost=False,isPlot=True):
    """
    实现一个L层神经网络：[LINEAR-> RELU] *（L-） - > LINEAR-> SIGMOID。

    参数：
        X - 输入的数据，维度为(n_x，例子数)
        Y - 标签，向量，0为非猫，1为猫，维度为(,数量)
        layers_dims - 层数的向量，维度为(n_y,n_h,···,n_h,n_y)
        learning_rate - 学习率
        num_iterations - 迭代的次数
        print_cost - 是否打印成本值，每100次打印一次
        isPlot - 是否绘制出误差值的图谱

    返回：
     parameters - 模型学习的参数。 然后他们可以用来预测。
    """
    np.random.seed()
    costs = []

    #随机初始化参数
    parameters = initialize_parameters_deep(layers_dims)

    for i in range(,num_iterations):
        AL , caches = L_model_forward(X,parameters) #前向传播

        cost = compute_cost(AL,Y) #成本计算

        grads = L_model_backward(AL,Y,caches) #后向传播

        parameters = update_parameters(parameters,grads,learning_rate) #更新参数

        #打印成本值，如果print_cost=False则忽略
        if i %  == :
            #记录成本
            costs.append(cost)
            #是否打印成本值
            if print_cost:
                print("第", i ,"次迭代，成本值为：" ,np.squeeze(cost))
    #迭代完成，根据条件绘制图
    if isPlot:
        plt.plot(np.squeeze(costs))
        plt.ylabel('cost')
        plt.xlabel('iterations (per tens)')
        plt.title("Learning rate =" + str(learning_rate))
        plt.show()
    return parameters

我们现在开始加载数据集,图像数据集的处理可以参照吴恩达课后作业学习1-week2-homework-logistic

train_set_x_orig , train_set_y , test_set_x_orig , test_set_y , classes = lr_utils.load_dataset()

train_x_flatten = train_set_x_orig.reshape(train_set_x_orig.shape[], -).T
test_x_flatten = test_set_x_orig.reshape(test_set_x_orig.shape[], -).T

train_x = train_x_flatten /
train_y = train_set_y
test_x = test_x_flatten /
test_y = test_set_y

数据集加载完成，开始正式训练：

layers_dims = [, , , , ] #  -layer model
parameters = L_layer_model(train_x, train_y, layers_dims, num_iterations = , print_cost = True,isPlot=True)

返回：

第  次迭代，成本值为： 0.715731513413713
第  次迭代，成本值为： 0.6747377593469114
第  次迭代，成本值为： 0.6603365433622127
第  次迭代，成本值为： 0.6462887802148751
第  次迭代，成本值为： 0.6298131216927773
第  次迭代，成本值为： 0.606005622926534
第  次迭代，成本值为： 0.5690041263975135
第  次迭代，成本值为： 0.519796535043806
第  次迭代，成本值为： 0.46415716786282285
第  次迭代，成本值为： 0.40842030048298916
第  次迭代，成本值为： 0.37315499216069037
第  次迭代，成本值为： 0.30572374573047123
第  次迭代，成本值为： 0.2681015284774084
第  次迭代，成本值为： 0.23872474827672593
第  次迭代，成本值为： 0.20632263257914712
第  次迭代，成本值为： 0.17943886927493544
第  次迭代，成本值为： 0.15798735818801213
第  次迭代，成本值为： 0.14240413012273928
第  次迭代，成本值为： 0.12865165997885833
第  次迭代，成本值为： 0.11244314998155475
第  次迭代，成本值为： 0.08505631034966661
第  次迭代，成本值为： 0.05758391198605767
第  次迭代，成本值为： 0.044567534546938604
第  次迭代，成本值为： 0.03808275166597662
第  次迭代，成本值为： 0.034410749018403006

图示：

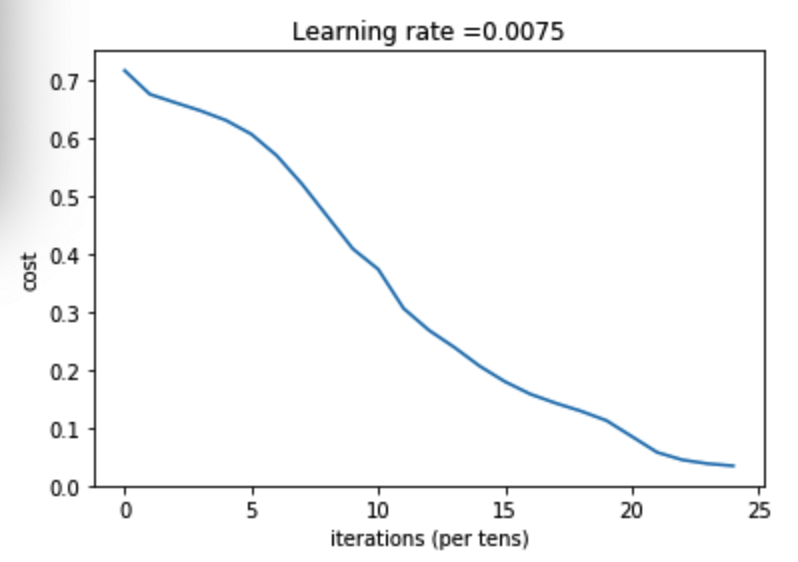
8.预测

def predict(X, y, parameters):
    """
    该函数用于预测L层神经网络的结果，当然也包含两层

    参数：
     X - 测试集
     y - 标签
     parameters - 训练模型得到的最优参数

    返回：
     p - 给定数据集X的预测
    """

    m = X.shape[1]
    n = len(parameters) // 2 # 神经网络的层数
    p = np.zeros((1,m))

    #根据参数前向传播
    probas, caches = L_model_forward(X, parameters)

    for i in range(0, probas.shape[1]):
        if probas[0,i] > 0.5:
            p[0,i] = 1
        else:
            p[0,i] = 0

    print("准确度为: "  + str(float(np.sum((p == y))/m)))

    return p

预测函数构建好了我们就开始预测，查看训练集和测试集的准确性：

pred_train = predict(train_x, train_y, parameters) #训练集
pred_test = predict(test_x, test_y, parameters) #测试集

返回：

准确度为: 0.9952153110047847
准确度为: 0.78

可见多层神经网络训练的效果比两层的要更好一些