【数据结构系列】线段树(Segment Tree)

一、线段树的定义

　　线段树，又名区间树，是一种二叉搜索树。

　　那么问题来了，啥是二叉搜索树呢？

　　对于一棵二叉树，若满足：

①它的左子树不空，则左子树上所有结点的值均小于它的根结点的值

②若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值

③它的左、右子树也分别为二叉搜索树

　　那么这就是一棵二叉搜索树。

　　扯完废话，再回到线段树这里。顾名思义，线段树就是由线段构成的树，它大概长成这样：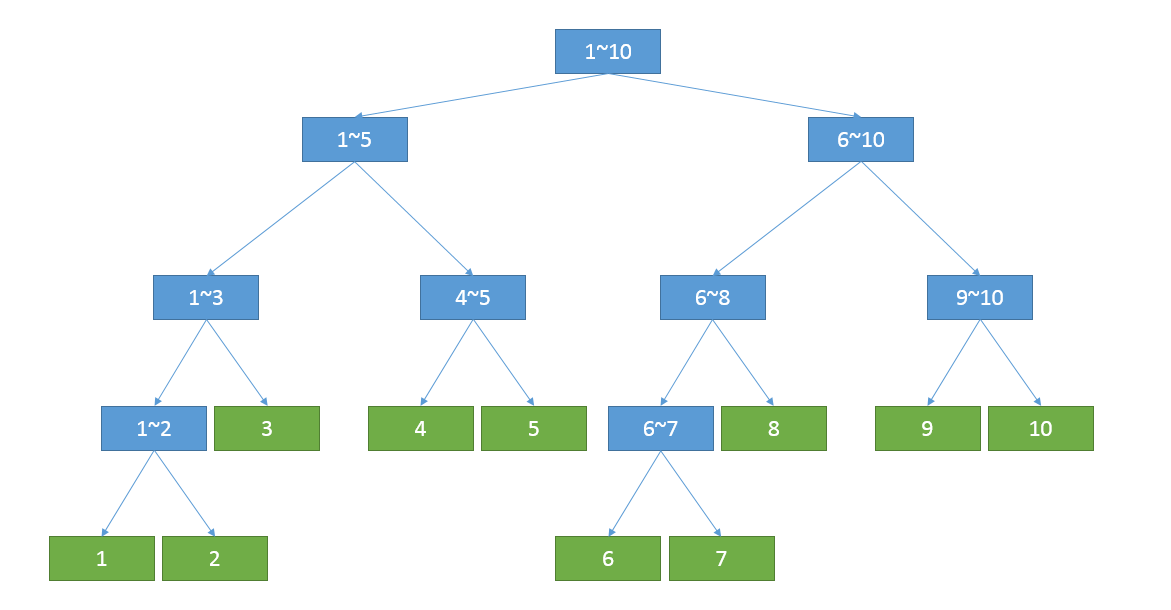

　　对于每一棵线段树上的节点，都有三个值：左区间、右区间以及权值。（当然，在某些情况下它只有左右区间，这个时候线段树只是作为维护某个值而使用的数据结构，如扫描线）

　　线段树有一个非常重要的性质，就是当父亲节点的区间为[x,y]时，左孩子的区间就必定为[x,(x+y)/2],右孩子的区间必定为[(x+y)/2+1,y]

二、线段树的基本操作

　　 常见的应用在竞赛中的操作分为：建树,单点修改,区间求和,查询区间最值,区间修改

　　我们先从建树开始讲起。

1.线段树的建树

　　线段树的建树是采用递归写法来构建的。其核心思想就是:

　　递归左子树，递归左子树的左子树...递归到左子树的叶子结点，然后回溯到叶子结点的父节点的右子树...以此类推。在每一次递归到叶子结点的时候就给该节点赋值（输入或者0之类的）。

　　建树的伪代码很容易得出:

 void Build() {
     if(是叶子节点) 赋值
     else {
         递归左子树;
         递归右子树;
     }
 }

　　  那么问题出在这里:怎么判断是叶子结点？怎么递归左右子树？现在，往上翻，看看线段树的性质。至于叶子节点的判断,我们也可以利用线段树的性质。叶子结点没有子节点，那么它的左右区间必定相同(即一个点而不是一条线段)，否则可以继续向下递归。

　　另外，线段树是一棵满二叉树，所以满足满二叉树一个性质:父亲节点编号为a,那么左子树编号为2*a,右子树编号为2*a+1

　　知道了这些性质，建树就很好写了。

 /*i表示当前递归编号,l,r分别表示当前点的左右区间*/
 /*Tree数组是存储线段树的数组*/
 void Build(int i, int l, int r) {
      if(l == r) {
          scanf("%d", Tree[i])
          return;
      }
      int Mid = (l + r) / ;
      Build(i * , l, Mid);
      Build(i * , Mid + , r);
      PushUp(i) /*这是什么?往后看*/
 }

　　 怎么样？很简单吧！

2.线段树的单点修改

　　接下来来讲讲线段树最基本操作之一 -- 单点修改。(前面讲了怎么递归左右子树，这里不再赘述)

　　单点修改在题目中一般以 "给定两个数A, B,将树上第A个修改为B"的形式存在。你可能认为:"这不是很Easy吗？"，然后立马敲下了这一段代码。

Tree[A] = B

　　这么写就大错特错了！因为这里的"Tree[A]"不一定是我们需要找的那个'A'，这么写的话会导致整棵树结构被打乱。

　　特别提醒:线段树中的修改操作一定只能使用特别的操作来完成，千万不要自以为是的写一些似乎是对的代码

　　那么怎么做呢?我们来分析一下。

　　如果要找到这个点A，我们必须要递归左右子树来寻找。上面介绍了递归的方法，大家是否已经发现了这样的递归很像某一种算法?没错，就是分治(如果要理解成二分也没有问题)，那么问题就很显然了，每次都二分，如果要寻找的点A在当前区间的中点，即(l+r)/2之前，就递归左子树，否则递归右子树。那么写成伪代码是这样的

void Quary_Single() {
  if(找到改点) 修改
  if(查找点在当前区间前半部分) 递归左子树
  else 递归右子树
}

　　这些操作我都介绍过了，那么写成真正的代码也不会很难吧。

 /*i为当前编号,L,R为左右区间,A为修改点的编号,B为修改的值*/
 void Update_Single(int i, int L, int R, int A, int B) {
     if(L == R) {
          /*如果找到了,修改值*/
          Tree[i] == B;
          return;
      }
      int Mid = (L + R) / ;
      if(A <= Mid) Update_Single(i * , L, Mid, A, B); /*递归左子树*/
      else Update_Single(i *  + , Mid + , R, A, B); /*递归右子树*/
      PushUp(i); /*这是什么?往后看*/
  }

　　大家应该都有一个想法吧:单点修改也不过如此。

　　的确，不过如此

3.线段树的区间求和

　　首先我要介绍一个东西，叫做 "PushUp"函数。这个函数的作用是什么呢?应该有很多人都想到了，就是将子节点的信息"传"给父亲节点。具体写起来也不难，我们可以将PushUp函数当做前缀和来处理(其实方便区间和，如果要求区间最值，PushUp函数就是处理最值了)

　　代码大约是这样:

/*区间最值处理*/
void PushUp(int Now) {
    Tree[Now] = Max(Tree[Now * ], Tree[Now *  + ]);
}
/*区间和处理*/
void PushUp(int Now) {
    Tree[Now] = Tree[Now * ] + Tree[Now *  + ];
}

　　这个东西要在什么地方加上呢?要在建树以及修改之后，也就是上述的两个操作之后。。

　 那么来讲讲区间求和问题吧。区间求和其实非常简单，我们只需要查询给定的区间，然后找到这个区间里面的所有叶子结点，把叶子结点的权值加起来，得到的结果就是我们所需要的区间和。那么要PushUp干嘛呢?PushUp简化了这个过程。在原本的操作里，最差的情况是要递归一直到叶子结点，多么令人心痛的浪费时间！然而我们用PushUp预处理之后，就变成了前缀和问题，求和不就是小菜一碟吗？

　 给出伪代码

int Quary_Total() {
    if(在查询区间内) 返回当前权值
    if(当前区间中点在查询区间的右边) 遍历左子树,并求和
    if(当前区间中点在查询区间的左边) 遍历右子树,并求和
    return 答案
}

　 真代码不需要我多说了吧。

 /*i 为当前编号, L, R为查询区间*/
 int Quary_Total(int i, int L, int R, int l, int r) {
      if(l >= L && r <= R) return Tree[i]; /*如果在区间内*/
      int Mid = (L + R) / , Cnt = ; /*初始化*/
      if(L <= Mid) Cnt += Quary_Total(i * , L, R, l, Mid); /*递归左子树*/
      if(R > Mid)  Cnt += Quary_Total(i *  + , L, R, Mid + , r); /*递归右子树*/
      return Cnt;
  }

　　就是这么简单。

4.线段树的区间最值

　 其实区间最值完全可以放在区间和里面讲的，因为写法几乎一样，唯一不同的是PushUp的方式以及判断的方式。因为在PushUp的时候预处理每一棵子树的最值，所以真正处理区间时只要把上面一层扫过去就可以了。

　 真代码直接上:)

int Quary_RMQ(int i, int L, int R, int l, int r) {
     if(l >= L && r <= R) return Tree[i];
     int Mid = (L + R) / , Cnt = ;
     int A, B;
     A = Quary_RMQ(i * , L, R, l, Mid);
     B = Quary_RMQ(i *  + , L, R, Mid + , R);
     return Max(A, B); /*返回最大值*/
 }

　那么线段树的四大基本操作就这么讲完了

三、线段树的优势和劣势

　　线段树的优势和劣势都很明显。

优势:时间快,操作多

　　线段树的优势首先是时间快，上文也讲过，线段树的所有操作都是基于分治算法，再经过PushUp优化，整个算法就变得十分稳定。比起一般的数组暴力算法，线段树是明显更优的。看下表就知道

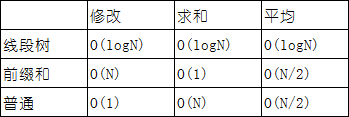
　　当然，在一些时候它也会劣于下面两种算法，不过是在极少数时候。

　 另外，它操作多样化，比起树状数组，多了区间最值一种操作。　　

劣势:空间浪费

　　上面也介绍过了,线段树一直是一棵满二叉树，所以无论如何，它所开的空间必须是四倍。但是在某些情况，线段树会浪费三倍的空间(只有一条链等),但你又不能省掉这三倍空间，还是得苦逼的开四倍。

　　和树状数组比起来，一棵普通的线段树是树状数组空间的四倍。

四、总结

　　线段树是一种区间存储结构，操作基本都有一个固定的模板，所以对于OIer的编码能力要求并不强，只要掌握了，基本就是小菜一碟。只要注意空间上的问题，其他都没什么困难的。

　谢谢大家的收看！如有不对之处请指出！ :)

　　本文作者: $xiaoyao24256$