使用经验风险最小化ERM方法来估计模型误差 开坑
虽然已经学习了许多机器学习的方法,可只有我们必须知道何时何处使用哪种方法,才能将他们正确运用起来。
那不妨使用经验最小化ERM方法来估计 。
首先:
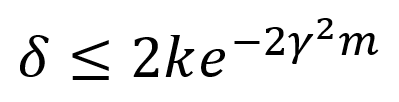
其中,
δ代表训练出错的概率
k代表假设类的个数
m代表样本(数据集)个数
γ代表误差阈值
于是我们可以得到:
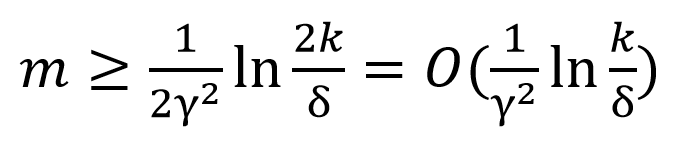
但我们的假设都是建立在k有限的条件上,那么如果Η为无限类,又该如何估计呢?
先说一个粗略结论:其实根据有限字长效应,我们知道,每个数最多有64字节,例如如果有d个特征,则:
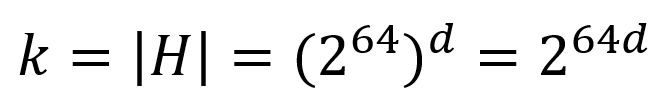
也就是说:
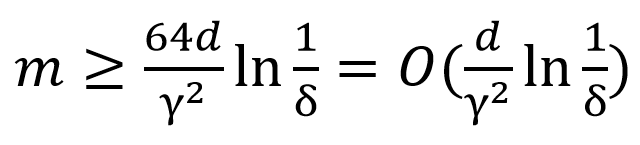
这个粗略结论已经比较实用了,不是吗。
其实,在现实情况中,不一定满足独立同分布的条件,因此真正的结果会比此结果乐观的多。具体的数字意义也不大,只需确定数量级即可。
不妨记住一个简答的结论:所需样本数量与VC维成正比
使用经验风险最小化ERM方法来估计模型误差 开坑的更多相关文章
- 【cs229-Lecture9】经验风险最小化
写在前面:机器学习的目标是从训练集中得到一个模型,使之能对测试集进行分类,这里,训练集和测试集都是分布D的样本.而我们会设定一个训练误差来表示测试集的拟合程度(训练误差),虽然训练误差具有一定的参考价 ...
- 机器学习理论基础学习3.3--- Linear classification 线性分类之logistic regression(基于经验风险最小化)
一.逻辑回归是什么? 1.逻辑回归 逻辑回归假设数据服从伯努利分布,通过极大化似然函数的方法,运用梯度下降来求解参数,来达到将数据二分类的目的. logistic回归也称为逻辑回归,与线性回归这样输出 ...
- 【Coursera】经验风险最小化
一.经验风险最小化 1.有限假设类情形 对于Chernoff bound 不等式,最直观的解释就是利用高斯分布的图象.而且这个结论和中心极限定律没有关系,当m为任意值时Chernoff bound均成 ...
- 文本分类学习 (七)支持向量机SVM 的前奏 结构风险最小化和VC维度理论
前言: 经历过文本的特征提取,使用LibSvm工具包进行了测试,Svm算法的效果还是很好的.于是开始逐一的去了解SVM的原理. SVM 是在建立在结构风险最小化和VC维理论的基础上.所以这篇只介绍关于 ...
- 【转载】VC维,结构风险最小化
以下文章转载自http://blog.sina.com.cn/s/blog_7103b28a0102w9tr.html 如有侵权,请留言,立即删除. 1 VC维的描述和理解 给定一个集合S={x1,x ...
- 机器学习理论基础学习4--- SVM(基于结构风险最小化)
一.什么是SVM? SVM(Support Vector Machine)又称为支持向量机,是一种二分类的模型.当然如果进行修改之后也是可以用于多类别问题的分类.支持向量机可以分为线性和非线性两大类. ...
- svm、经验风险最小化、vc维
原文:http://blog.csdn.net/keith0812/article/details/8901113 “支持向量机方法是建立在统计学习理论的VC 维理论和结构风险最小原理基础上” 结构化 ...
- Effective Java 第三版——74. 文档化每个方法抛出的所有异常
Tips 书中的源代码地址:https://github.com/jbloch/effective-java-3e-source-code 注意,书中的有些代码里方法是基于Java 9 API中的,所 ...
- 机器学习 之 SVM VC维度、样本数目与经验风险最小化的关系
VC维在有限的训练样本情况下,当样本数 n 固定时.此时学习机器的 VC 维越高学习机器的复杂性越高. VC 维反映了函数集的学习能力,VC 维越大则学习机器越复杂(容量越大). 所谓的结构风险最小化 ...
随机推荐
- LINUX下安装pcre出现WARNING: 'aclocal-1.15' is missing on your system错误的解决办法
1.下载安装包 wget https://ftp.gnu.org/gnu/automake/automake-1.15.tar.gz 2.解压 tar -xzvf automake-1.15.tar. ...
- vue.js数组追加合并与对象追加合并的
今天在做懒加载的时候遇到的问题,在网上搜索找到的答案不是很清晰,就来写一下,方便以后使用. 直接上图吧 官方连接:https://cn.vuejs.org/v2/guide/reactivity.ht ...
- 京东7Fresh新零售架构设计分析
7Fresh是京东第一个线上线下融合落地的零售创新业务模式,店内有大量设备的集成,设备供应商达50多家,针对线下业务的特点,团队独立规划和设计POS收银系统.店内生产系统.加工系统.货架陈列系统.魔镜 ...
- MySQL索引优化经验总结
1.对查询进行优化,应尽量避免全表扫描,首先应考虑在 where 及 order by 涉及的列上建立索引. 2.尽量避免在 where 子句中对字段进行 null 值判断,否则将导致引擎放弃使用索引 ...
- plsql developer 64位 注册码
注册码product code(产品编码): 4vkjwhfeh3ufnqnmpr9brvcuyujrx3n3le serial Number(序列号):226959 password(口令): xs ...
- No MyBatis mapper was found in '[com.wuji.springboot]' package. Please check your configuration
No MyBatis mapper was found in '[com.wuji.springboot]' package. Please check your configuration. 这个原 ...
- #leetcode刷题之路23-合并K个排序链表
合并 k 个排序链表,返回合并后的排序链表.请分析和描述算法的复杂度. 示例:输入:[ 1->4->5, 1->3->4, 2->6]输出: 1->1->2- ...
- CentOS6安装各种大数据软件 第十章:Spark集群安装和部署
相关文章链接 CentOS6安装各种大数据软件 第一章:各个软件版本介绍 CentOS6安装各种大数据软件 第二章:Linux各个软件启动命令 CentOS6安装各种大数据软件 第三章:Linux基础 ...
- Ajax数据获取(未完待续。。。)
@:网站内容通过Ajax获取数据然后重新渲染产生 这种时候我们如何拿到自己想要的数据: 1:打开检查,在network选项中查看浏览器发送了哪些请求.(清空,再刷新,得到新的请求) 在截图的左下角可以 ...
- XML第一次简单入门(Lab分析)
In this tutorial you will create a well-formed and verified XML file. Consider the XML document belo ...
