CF932E Team Work——第二类斯特林数

题解

n太大，而k比较小，可以O(k^2)做

想方设法争取把有关n的循环变成O(1)的式子

考虑用公式：

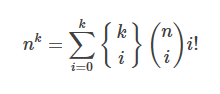
来替换i^k

原始的组合数C(n,i)一项，考虑能否和后面的系数分离开来，直接变成2^n处理。

之后大力推式子

考虑要消掉n，就想办法把n往里面放，与和n有关的项外层枚举的话，相对就不动了。可以乘法分配律把n搞定。

#include<bits/stdc++.h>
#define reg register int
#define il inline
#define numb (ch^'0')
using namespace std;
typedef long long ll;
il void rd(int &x){
    char ch;x=;bool fl=false;
    while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true);
    for(x=numb;isdigit(ch=getchar());x=x*+numb);
    (fl==true)&&(x=-x);
}
namespace Miracle{
const int N=;
const int mod=1e9+;
int s[N][N];
int C[N][N];
ll qm(ll x,ll y){
    ll ret=;
    while(y){
        if(y&) ret=ret*x%mod;
        x=x*x%mod;
        y>>=;
    }
    return ret;
}
ll n,k;
int main(){
    scanf("%lld %lld",&n,&k);
    if(n>k){
        s[][]=;
        for(reg i=;i<=k;++i){
            for(reg j=;j<=k;++j){
                s[i][j]=((ll)s[i-][j-]+(ll)j*s[i-][j]%mod)%mod;
            }
        }
        ll jie=;
        ll ans=;
        for(reg j=;j<=k;++j){
            jie=jie*(n-j+)%mod;
            ll mi=qm(,n-j);
            ans=(ans+(ll)s[k][j]*jie%mod*mi%mod)%mod;
        }
        printf("%lld",ans);
    }else{
        C[][]=;
        for(reg i=;i<=n;++i){
            C[i][]=;
            for(reg j=;j<=n;++j){
                C[i][j]=((ll)C[i-][j]+C[i-][j-])%mod;
            }
        }
        ll ans=;
        for(reg i=;i<=n;++i){
            ans=(ans+(ll)C[n][i]*qm(i,k))%mod;
        }
        printf("%lld",ans);
    }
    return ;
}

}
signed main(){
    Miracle::main();
    return ;
}

/*
   Author: *Miracle*
   Date: 2018/12/28 19:46:50
*/

推式子其实是下策（下下策是打表找规律。。。）

如果有组合意义的话，那么效果是立竿见影的。

意义是，n个盒子，从中选择i个出来，再把k个球往这i个盒子里放，可以不放的方案数总和。盒子不同球不同

k很小，没用的盒子很多，

转化研究对象，

考虑k个球最终占据了哪几个盒子。其他的盒子打酱油爱选不选。

那么直接就是：

一步搞定！