[蓝桥杯]PREV-19.历届试题_九宫重排

题目描述：

代码如下：

 #include <stdio.h>
 #include <stdlib.h>
 #include <string.h>
 #define N  1000000
 #define HN 1000003
 #define LEN 9

 int head[HN],next[N];
 int st[N][LEN], goal[LEN];
 int dis[N];    //记录步数 

 int Hash(int *st)//获取本次排列组合的哈希值
 {
     int i,v;
     v = ;
     for (i= ; i<LEN ; i++)//得到一个LEN长度数值：v
     {
         v = v* + st[i];
     }
     return v%HN;//得到对应哈希值
 }

 // 功能：对本次的排列组合，若不在哈希表中，则在哈希表中进行键值映射
 int try_insert(int rear)//rear：本次组合的编号
 {
     int h = Hash(st[rear]);    //获得本次排列组合对应的哈希值
     int u = head[h];        //根据哈希值，获得哈希表中对应的键(key),若没有则为0 

     while (u)//当上一步有拿到键(key),查找对应的值(value->排列组合),
     {
         if (memcmp(st[u],st[rear],sizeof(st[]))==)//存在相同的值(value->排列组合)
             return ;    //本次值(value->排列组合)将不记录，退出
         u = next[u];    //当前键(key)还有其他值，遍历获得其他值(value->排列组合)
     }

     //当前值(value->排列组合)不在哈希表中，将进行记录
     next[rear] = head[h];    //当前键(key)的记录是否有其他值，若本身为新组合，为0；若为存在组合，则为其上一个编号(相同组合)
     head[h] = rear;            //哈希表中对应的键(key)，更新为本次组合编号(rear)
     return ;
 }

 int bfs()
 {
     int d;
     int x,y,z,nx,ny,nz;
     int fron = ,rear = ;    //fron：当前排列组合；rear：移动后的排列组合
     const int dir[][] = {{,},{,-},{,},{-,},};

     memset(head,,sizeof(head));
     while (fron < rear)
     {
         if (memcmp(goal,st[fron],sizeof(st[]))==)//当前排列组合为目标排列组合
             return fron; 

         for (z= ; z<LEN ; z++)
         {
             if (st[fron][z]==)//0即为对应的'.'
                 break;
         }

         x = z/,y = z%;//获得'.'的坐标
         for (d= ; d< ; d++)
         {
             nx = x+dir[d][];
             ny = y+dir[d][];
             if (nx>= && nx< && ny>= && ny<)
             {
                 nz = *nx+ny;//'.'将要移动的下一步位置 

                 memcpy(&st[rear],&st[fron],sizeof(st[]));
                 st[rear][nz] = st[fron][z];
                 st[rear][z] = st[fron][nz];

                 dis[rear] = dis[fron]+;//记录步数
                 if (try_insert(rear))//对新排列组合进行查找
                     rear ++;//进队列
             }
         }
         fron ++;//出队列
     }

     return ;
 }

 int main(void)
 {
     int i,ans;
     char s1[LEN+],s2[LEN+];
     memset(dis,,sizeof(dis));
     scanf("%s%s",&s1,&s2);

     for (i= ; i<LEN ; i++)//将'.'转换为0，便于计算哈希值
     {
         if (s1[i]=='.')
             st[][i] = ;
         else
             st[][i] = s1[i]-'';

         if (s2[i]=='.')
             goal[i] = ;
         else
             goal[i] = s2[i]-'';
     }    

     ans = bfs();
     if (ans > )
         printf("%d",dis[ans]);
     else
         puts("-1");

     return ;
 }

C解法

解题思路：

本题要求最少步数转换成目标组合，广度优先遍历(BFS)可满足要求

每次对新组合进行检查时，需要较高的检索效率，

1.使用map或者set做检索时，其对应的检索效率低，超时不能满足题目需求；

2.对组合进行哈希判重，大大提高了检索效率；

关于本题的哈希判重，参考了：

https://blog.csdn.net/hao_zong_yin/article/details/62419919

https://www.cnblogs.com/acxblog/p/7253477.html

哈希判重，利用键-值映射，有效提高了搜索的效率；

1.建立键(key)表，head[NH]，需初始化；建立值(value)表，next[N]；

2.BFS搜索新组合，通过向不同方向移动 ' . ' (0)  得到新的组合；

3.根据新组合，计算对应的哈希值；

4.根据哈希值，进行检索决定是否添加新的排列组合

　　4.1.插入的组合存在

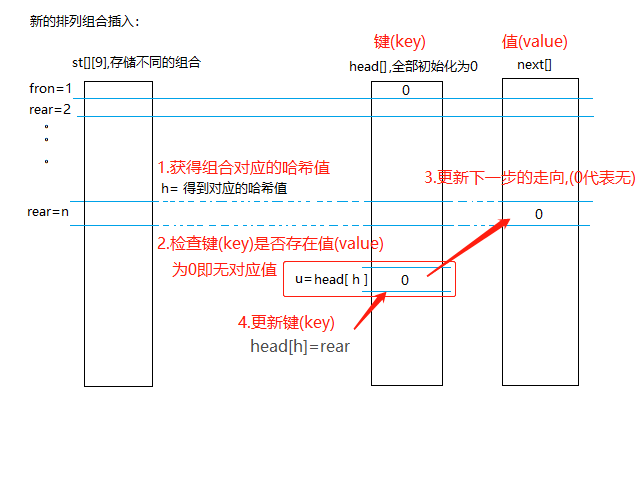
　　4.2.插入的组合不存在

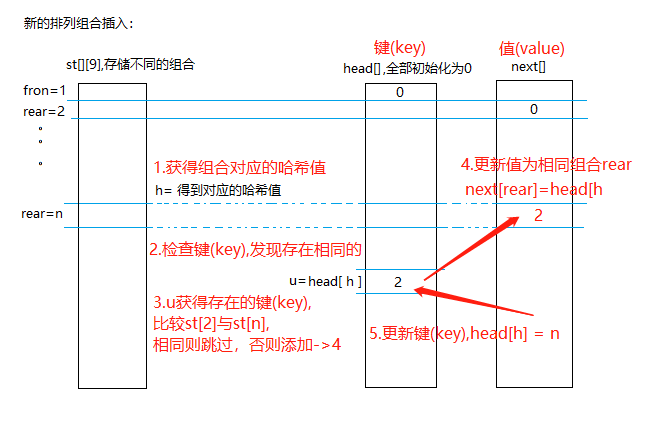
5.若有新组合添加，队列+1（rear+1）

6.每次出列(fron+1)，检查是否为目标组合

7.若fron > rear，则不存在方案，输出-1