找一个数组的最大和的连续子数组(时间复杂度 O(n))

设计思想

一开始的思想是求出全部的情况，再分别比较大小，这种方法适用于有限个数组，不适用于输入数组长度和内容的情况。

但也试着做了

 int a[]= {-1,2,6,-10};
         int size=4;
                 int maxa=a[0];
         for(int i=0;i<size;i++) {
             if(maxa<a[i])
                 maxa=a[i];
         }
         //对于两个数一组
         int b[]=new int[size-1];
         for(int i=0;i<size-1;i++) {
             b[i]=a[i]+a[i+1];
         }
         //再遍历b数组
         int maxb=b[0];
         int sizeb=size-1;
         for(int i=0;i<sizeb;i++) {
             if(maxb<b[i])
                 maxb=b[i];
         }
         //对于三个数一组
         int c[]=new int[size-2];
         int sizec=size-2;
         for(int i=0;i<sizec;i++) {
             c[i]=a[i]+a[i+1]+a[i+2];
         }
         //再遍历c数组
         int maxc=c[0];
         for(int i=0;i<sizec;i++) {
             if(maxc<c[i])
                 maxc=c[i];
         }
         //对于四个数一组
         int maxd=0;
         for(int i=0;i<size;i++) {
             maxd=maxd+a[i];
         }

         //比较这些组合的大小
         int max1=0;
         int max2=0;
         int max=0;
         if(maxa>maxb) {
             max1=maxa;
         }else {
             max1=maxb;
         }
         if(maxc>maxd) {
             max2=maxc;
         }else {
             max2=maxd;
         }
         if(max1>max2) {
             max=max1;
         }else {
             max=max2;
         }
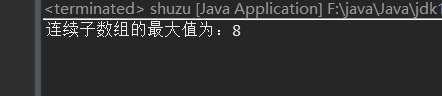
         System.out.println("连续子数组的最大值为："+max);                 

这种方法比较傻，下面是我参考了网上的之后自己动手解决的。

设计思想：

把最大值sum赋值为0，curr是当前数值，curr=curr+下一个数  依次类推，若curr为负数，就让curr

为0，否则就判断sum和curr的大小关系，sum=较大的那个数。

         Scanner sc=new Scanner(System.in);
         //定义数组长度和数组
         //输入数组长度
         System.out.println("请输入数组的长度:");
         int size=sc.nextInt();
         int a[]=new int[size];
         int sum=0;
         int curr=0;

         //输入数组的内容
         System.out.println("请输入数组内容:");
         for(int i=0;i<size;i++) {
             a[i]=sc.nextInt();
         }

         //有负有正
         for(int i=0;i<size;i++) {
             curr=curr+a[i];
             if(curr<0) {
                 curr=0;
             }else {
                 if(sum<curr) {
                     sum=curr;
                 }else {
                     sum=sum;
                 }
             }
         }
         //若全是是负数
         if(sum==0) {
             int sum1=a[0];
             for(int i=0;i<size-1;i++) {
                 if(sum1>a[i+1]) {
                     sum1=sum1;
                 }
                 else {
                     sum1=a[i+1];
                 }
             }
             sum=sum1;
         }

         System.out.println("连续子数组的最大值为："+sum);

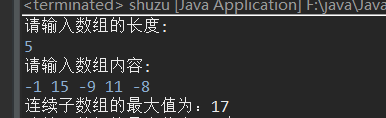
全是负数的情况

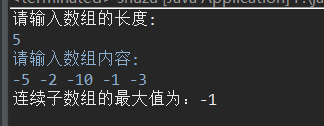
遇到的问题：

1，最开始没有比较curr和sum的大小关系，而直接让sum=curr，会导致sum为最后一个为正的数

2，忘记考虑全是负数的情况，导致全为负数，sum的值=0。

总结：

在设计此类题的时候，要考虑周到，在时间复杂度为o(n)的条件下，把各种情况都要考虑到。

还要多尝试，写出来代码出错后要一步一步推敲错在哪里，分析分解，再锁定错的地方，是解决问题的关键。