https://en.wikipedia.org/wiki/Frenet%E2%80%93Serret_formulas

The tangent, normal, and binormal unit vectors, often called T, N, and B, or collectively the Frenet–Serret frame or TNB frame, together form an orthonormal basis spanning ℝ3 and are defined as follows:

  • T is the unit vector tangent to the curve, pointing in the direction of motion.
  • N is the normal unit vector, the derivative of T with respect to the arclength parameter of the curve, divided by its length.
  • B is the binormal unit vector, the cross product of T and N.

切线空间中的T（tangent），B（Bitangent）与贴图U，V方向一致。 保存方式（T,B,N）

Normal

T（tangent）

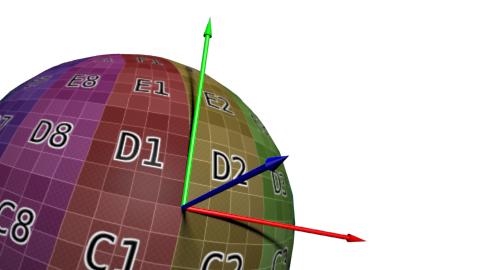
B（Bitangent）  = N*T

Tangent space(切线空间)的更多相关文章

  1. 切线空间（Tangent Space）法线映射（Normal Mapping）【转】

    // 请注明出处:http://blog.csdn.net/BonChoix,谢谢~) 切线空间(Tangent Space) 切换空间,同局部空间.世界空间等一样,是3D图形学中众多的坐标系之一.切 ...

  2. 3D中的切线空间简介

    转自:http://www.cnblogs.com/cxrs/archive/2009/10/25/1589515.html 1. 什么是Tangent space? Tangent space和wo ...

  3. tangent space与object space

    3d渲染每个网格(Mesh)的面都可配一个材质(Material),要想在一个面上显示出更多的细节,除了模型做的更精致,还可以使用法线贴图(Normal Texture). 法线向量(Normal V ...

  4. Unity shader学习之切线空间下计算凹凸映射

    切线空间,即使用顶点的切线作为x轴,法线作为z轴,法线与切线的叉积作为y轴. 使用切线空间存储法线,使得法线纹理可以复用,很好. 在切线空间中计算光照,比在世界空间中计算光照少了很多计算量.在切线空间 ...

  5. Normal Map中的值， Tangent Space， 求算 Tangent 与 Binormal 与 TBN Matrix

      - Normal Map中的值 -   有没有想过,Normal Map(法线贴图)为什么看上去都是“偏蓝色”的?这是因为,在map中存储的值都是在Tangent Space(切空间)下的.比如, ...

  6. [转]Normal Map中的值， Tangent Space， 求算 Tangent 与 Binormal 与 TBN Matrix

    原文出处 https://www.cnblogs.com/lookof/p/3509970.html - Normal Map中的值 -   有没有想过,Normal Map(法线贴图)为什么看上去都 ...

  7. 引擎设计跟踪(九.14.2a) 导出插件问题修复和 Tangent Space 裂缝修复

    由于工作很忙, 近半年的业余时间没空搞了, 不过工作马上忙完了, 趁十一有时间修了一些小问题. 这次更新跟骨骼动画无关, 修复了一个之前的, 关于tangent space裂缝的问题: 引擎设计跟踪( ...

  8. tangent space /handness

    normal tangent bitangent 三者互相垂直. 组成一个tangent space 表示一个点 对于原本位置的偏移(扰动) 考虑到这是为了 normalmap做出虚假的normal来 ...

  9. [Unity Shader] 切线空间的法线贴图

    切线空间的法线贴图,可以这样理解: #纹理坐标是从0到1,它的坐标是x向右,y向下 #顶点坐标是从-1到-1,坐标是x向右,y向上 1 由表面上某点的切线Tangent.副切线Bitangent.法线 ...

随机推荐

  1. [JavaScript] Imitate String.Format() in c#

    Definition if (!String.prototype.format) { String.prototype.format = function () { var args = argume ...

  2. node.js实现国标GB28181设备接入的sip服务器解决方案

    方案背景 在介绍GB28181接入服务器的方案前,咱们先大概给大家介绍一下为什么我们选择了用nodejs开发国标GB28181的服务,我大概给很多人介绍过这个方案,大部分都为之虎躯一震,nodejs在 ...

  3. sqlserver删除所有表

    --/第1步**********删除所有表的外键约束*************************/ DECLARE c1 cursor for select 'alter table ['+ o ...

  4. 右键打开cmd

    Windows Registry Editor Version 5.00 [HKEY_CLASSES_ROOT\Directory\shell\OpenCmdHere]@="Open cmd ...

  5. spring mvc 基本原理

    在web.xml配置spring mvc入口servlet: <servlet> <servlet-name>mvc-dispatcher</servlet-name&g ...

  6. Android 开发之深入理解安卓调试桥各种错误解决办法

    摘要: Android开发调试项目使用到安卓调试桥工具,Android Debug Bridge(ADB)位于sdk路径platform-tools文件夹,使用Android Studio或Eclip ...

  7. 用VirtualBox和vagrant在win7&#215;64上搭建ruby on rails 开发环境

    下载准备 1.vagrant 官方  WINDOWS Universal (32 and 64-bit) http://www.vagrantup.com/downloads.html 2.Virtu ...

  8. Linux c编程：I/O多路复用之epoll

    前面介绍了select处理,这一章继续介绍另外一种I/O多路服用的机制:epoll.来比较下两种机制的不同点. select: 调用过程如下: (1)使用copy_from_user从用户空间拷贝fd ...

  9. 拉普拉斯分布（Laplace distribution）

    拉普拉斯分布的定义与基本性质 其分布函数为 分布函数图 其概率密度函数为 密度函数图 拉普拉斯分布与正太分布的比较 从图中可以直观的发现拉普拉斯分布跟正太分布很相似,但是拉普拉斯分布比正太分布有尖的峰 ...

  10. eclipse安装Activiti Designer插件(转载：http://blog.csdn.net/qq_33547950/article/details/54926435)

    为了完成毕业设计,需要学习Activiti.万事开头难,果然刚开始就遇到了问题.<Activiti实战>和视频教程里提供的安装Activiti Designer插件方法(即下文方法一)不能 ...