python算法题 python123网站单元四题目

目录

• 一：二分法求平方根
  • 1.题目要求为
  • 2.输入输出格式为
  • 3.博主解题的思路
  • 4.代码如下
    • (1)循环解题代码
    • (2)递归解题代码
• 二：Collatz猜想
  • 1.题目要求为
  • 2.输入输出格式为
  • 3.博主解题的思路
  • 4.代码如下
    • (1)循环解题代码
    • (2)递归解题代码
• 三：算24(只考虑满足，不考虑把所有情况找出来)
  • 1.题目要求为
  • 2.输入输出格式为
  • 3.博主解题的思路
    • (1)常规方法
  • 4.代码如下
    • (1)普通方法

  下面向大家介绍几个python算法题。

一：二分法求平方根

1.题目要求为

2.输入输出格式为

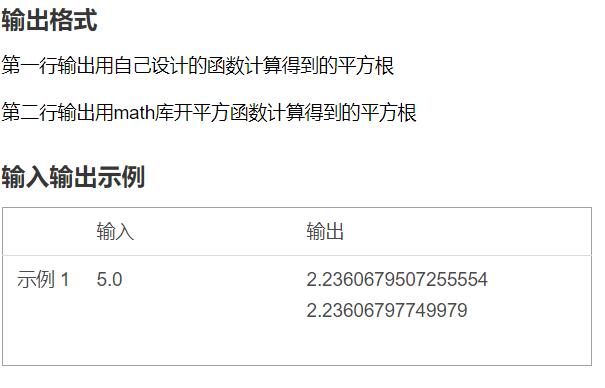
3.博主解题的思路

  这道题在c语言中是一道经典的题目，可以用循环，或者递归，在这里我们用python来写。无论是循环还是递归，都是下面的思路：

  二分法就是从中间开始取，把我们每次的结果的变化值(这里是平方)和初始数值对比，然后分别从左右两边截取。

  这里首先设定两个范围定界符low与high，而且有可能我们输入法的小于1，就需要语法max(n,1.0)，然后得到每次的中间值mid，然后进行循环或者递归，条件是，我们最终的得到的平方根mid的平方和我们最初的数值n的相差范围在1e-6。

  然后根据mid的平方和n对比，如果mid的平方小于n的话，说明n的平方根在原来中间值的右边，此时就要在中间值以及最大值的那个范围寻找，把下一次的初始值设为前一次的中间值，然后前一次的中间值取下一次的中间值；如果如果mid的平方大于n的话，刚好反过来，这样等到循环到mid的平方和我们最初的数值n的相差范围在1e-6时，就可以认为结果在合理范围内。

4.代码如下

(1)循环解题代码

from math import sqrt

def sqrt_binary(n):
	low = 0
	high = max(n,1.0)
	mid = (high + low) / 2.0

	while abs(mid ** 2 - n) > 1e-6:
		if mid ** 2 < n:
			low = mid
		else:
			high = mid
		mid = (high + low) / 2.0
	print(mid)
	print(sqrt(n))

n = eval(input(""))
sqrt_binary(n)

(2)递归解题代码

from math import sqrt

def sqrt_binary(n,low,high,mid):
	if abs(mid ** 2 - n) <= 1e-6:
		print(mid)
		print(sqrt(n))
	else:
		if mid ** 2 < n:
			low = mid
			mid = (high + low) / 2.0
			sqrt_binary(n,low,high,mid)
		else:
			high = mid
			mid = (high + low) / 2.0
			sqrt_binary(n,low,high,mid)

n = eval(input(""))
low = 0
high = max(n,1.0)
mid = (high + low) / 2.0
sqrt_binary(n,low,high,mid)

二：Collatz猜想

1.题目要求为

2.输入输出格式为

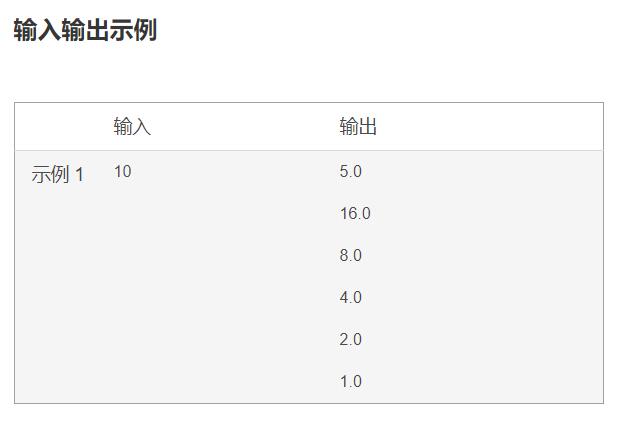
3.博主解题的思路

  这是一道十分简单的题目，我们可以用循环或递归对不同的情况判断即可。

4.代码如下

(1)循环解题代码

n = eval(input(""))

while n != 1:
	if n % 2 == 0:
		n /= 2
		print('%.1f' % n)
	else:
		n = 3 * n + 1
		print('%.1f' % n)

(2)递归解题代码

n = eval(input(""))

def get(n):
	if n != 1:
		if n % 2 == 0:
			n /= 2
			print('%.1f' % n)
			get(n)
		else:
			n = 3 * n + 1
			print('%.1f' % n)
			get(n)

get(n)

三：算24(只考虑满足，不考虑把所有情况找出来)

1.题目要求为

2.输入输出格式为

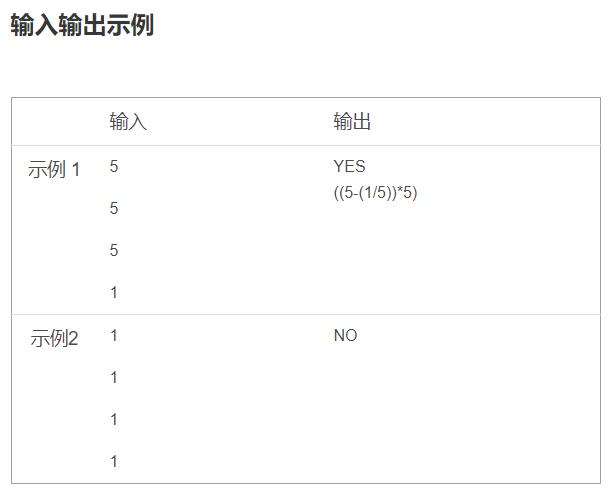
3.博主解题的思路

  这里首先要考虑怎样用数学的方法判断4个数字是否可以得带24，在考虑用程序如何实现。

(1)常规方法

   数学方法算24：

  这里其实可以穷举，抽象四个数为n1,n2,n3,n4，然后考虑和符号配合的情况，然后一次再和四个数进行配合，但是可能比较繁琐，不太提倡这种方法。

   程序思路(繁琐的方法)：

  计算顺序有下面的五种：

  ((n1 运算符1 n2) 运算符2 n3) 运算符3 n4

  n4 运算符3 ((n1 运算符1 n2) 运算符2 n3)

  (n3 运算符2 (n1 运算符1 n2)) 运算符3 n4

  n4 运算符3 (n3 运算符2 (n1 运算符1 n2))

  (n1 运算符1 n2) 运算符3 (n3 运算符2 n4)

  而4个操作数有4 * 3 * 2 * 1 = 24种排序。

  对于n1 n2 n3 n4中间的操作数，每个位置有加减乘除四种运算符，不考虑括号，有4 * 4 * 4 = 64种搭配。

  接下来就需要编程了，有下面的步骤：

  外层循环，对24种数字排序组合

  内层循环，对64种运算符排列组合

  循环内部，分别按照5种运算顺序(带括号)，进行计算，然后判断结果是否等于24，得到结果，输出YES与搭配，否则输出ERROR。

   这种方法可以得到所有可能的结果。但是要进行小数除法。

4.代码如下

(1)普通方法

from itertools import permutations

def run_operators(a,op,b):
	"""
	这里简化说明，是每一步的操作
	"""
	result = 0.0
	num1 = float(a)
	num2 = float(b)
	if op == '+':
		result = num1 + num2
	elif op == '-':
		result = num1 - num2
	elif op == '*':
		result = num1 * num2
	else:
		if num2 == 0:
			result = 9999999999999	#这里无限大，避免出错
		else:
			result = num1 / num2
	return result

def main():
	n1 = eval(input(""))
	n2 = eval(input(""))
	n3 = eval(input(""))
	n4 = eval(input(""))

	# 如果输入[0,9]范围之外，就会报错
	if n1 < 0 or n2 < 0 or n3 < 0 or n4 < 0 or n1 > 9 or n2 >9 or n3 > 9 or n4 > 9:
		print("NO")

	num = []
	# 24种操作数排列组合,用二维列表表示
	for i in list(permutations([n1, n2, n3,n4], 4)):
		num.append(list(i))

	opt = []
	operators = ['+','-','*','/']
	# 64种运算符排列组合生成，用二维列表表示
	for i in range(0,4):
		for j in range(0,4):
			for k in range(0,4):
				opt.append([operators[i],operators[j],operators[k]])

	str1 = ""
	# 下面是最终的运算判断以及排列组合
	for n in num:
		for p in opt:
			# ((n1 运算符1 n2) 运算符2 n3) 运算符3 n4
			result = run_operators(run_operators(run_operators(n[0],p[0],n[1]),p[1],n[2]),p[2],n[3])
			if int(result) == 24:
				str1 = 'YES'
				print('YES')
				print("{0}{1}{2}{3}{4}{5}{6}{7}{8}{9}{10}{11}".format("(","((",n[0],p[0],n[1],")",p[1],n[2],")",p[2],n[3],")"))
				exit()
			# n4 运算符3 ((n1 运算符1 n2) 运算符2 n3)
			result = run_operators(n[3],p[2],run_operators(run_operators(n[0],p[0],n[1]),p[1],n[2]))
			if int(result) == 24:
				str1 = 'YES'
				print('YES')
				print("{0}{1}{2}{3}{4}{5}{6}{7}{8}{9}{10}{11}".format("(",n[3],p[2],"((",n[0],p[0],n[1],")",p[1],n[2],")",")"))
				exit()
			# (n3 运算符2 (n1 运算符1 n2)) 运算符3 n4
			result = run_operators(run_operators(n[2],p[1],run_operators(n[0],p[0],n[1])),p[2],n[3])
			if int(result) == 24:
				str1 = 'YES'
				print('YES')
				print("{0}{1}{2}{3}{4}{5}{6}{7}{8}{9}{10}{11}".format("(","(",n[2],p[1],"(",n[0],p[0],n[1],"))",p[2],n[3],")"))
				exit()
			# n4 运算符3 (n3 运算符2 (n1 运算符1 n2))
			result = run_operators(n[3],p[2],run_operators(n[2],p[1],run_operators(n[0],p[0],n[1])))
			if int(result) == 24:
				str1 = 'YES'
				print('YES')
				print("{0}{1}{2}{3}{4}{5}{6}{7}{8}{9}{10}{11}".format("(",n[3],p[2],"(",n[2],p[1],"(",n[0],p[0],n[1],"))",")"))
				exit()
			# (n1 运算符1 n2) 运算符3 (n3 运算符2 n4)
			# result = run_operators(run_operators(n[0],p[0],n[1]),p[2],run_operators(n[2],p[1],n[3]))
			# if int(result) == 24:
			# 	str1 = 'YES'
			# 	print('YES')
			# 	print("{0}{1}{2}{3}{4}{5}{6}{7}{8}{9}{10}{11}".format("(","(",n[0],p[0],n[1],")",p[2],"(",n[2],p[1],n[3],")",")",end=""))
			# 	break
	if str1 == '':
		print('NO')

main()

  结果如下：