此篇文章源自对一个有趣问题的思考，在我的另一篇博文《一个有趣的 5 X 5 方阵一笔画问题》中有详细介绍。在已知其结论的情况下，作为程序员的我，还是想利用该问题当做出发点，写一个可以遍历所有“可能路线”的寻路算法，当做学习“图”相关算法的练习。如果对那个原始问题有兴趣，点击上面的文章链接，出门右转便是。

一、问题回顾

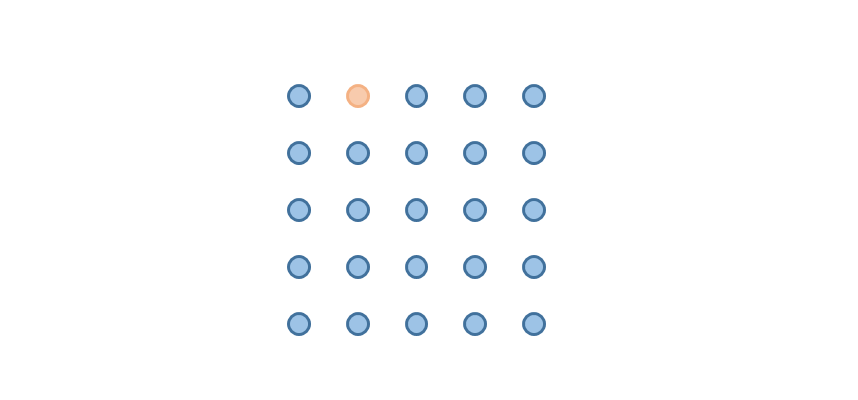
  还是要简单描述一下问题：有一个 5 X 5 的点方阵，如下图，要想用一笔画将所有的蓝色点连起来，是否有可行路线。需要满足3点要求：

  1、笔画必须水平或垂直。

  2、笔画不可以超出方阵边界之外，

  3、每个点只经过一次，且不可以经过黄色点。

  这个问题的数学证明已经在开头的文章中给出，在此不做赘述。这里只考虑它的算法实现。



  在思考算法之前，需要先对问题进行抽象分析，我们可以将上面的问题理解成下图这样 ：

二、抽象分析

  由于题目已经被数学证明没有一条路线能够满足题目要求，所以算法的目的不是为了找到所谓符合要求的路线，而是遍历从出发点向网格中所有点可形成的所有路线。可以假设上面的网格是一个地图，小明同学按照地图在网格中行走，目的是找出从出发点到所有点的所有路线。小明先在地图中规定坐标，网格底边作为x轴，左侧的竖边作为y轴，那么红色五角星坐标就是（1,4）。小明从原点开始出发，刚开始时地图中所有的交叉点都被标记“未走过”标识。小明随机选择下一个点，假如依次经过（0,0）、（1,0）、（1,1）、（2,1）、（2,2）、（3,2）、（4,2）、（4,1）、（4,0）、（3,0）、（3,1），每往前走一个点，他都会在地图的相应位置标记已经走过。走到（3,1）时，由于四周的（2,1）、（3,2）、（4,1）都已经走到过，所以往前是无路可走的，只能逐步回退，回退之前小明为了下次不再重新走这个线路，他将这个线路记到了本子上，并标记本路线为历史路线，然后回退，每回退一步小明都会在离开的那个位置将“已走过”的标记涂抹掉并改为“未走过”标识，因为这样当下次从其他路线走时还可以走那个位置。当回退到（3,0）时，（3,1）位置就会由标记“已走过”改为标记“未走过”的状态，并发现临近的（2,0）还没有走过，于是不再回退，转向（2,0）。到达（2,0）时，又出现了无路可走的情况，于是记录当下的路线，然后回退并标记地图。当回退到（3,0）时，虽然会发现（3,1）是“未走过”状态，但由于如果走（3,1）的话就会发现这条路线在笔记本的历史路线中已经出现过，所以依然不能走（3,1），继续回退，按照这个原则一直走下去，直到遍历完从起点出发到达地图上所有点的所有路线，小明最终一定会回到起点。此时他笔记本中的历史路线列表，就是从起点达地图上所有点的所有路线。

三、算法分析

  考虑到算法的实现，这显然是利用了数据结构中的“图”。每一次路线尝试，都是对图的深度遍历，算法要做的事情，无非就是随机选择起点，然后不断地深度遍历新的路线。每往前走一步，就将新位置放进栈。这里要注意的是，针对每一次尝试，当走到无路可走时，并不意味着24个点全部已经遍历到了，因为根据规则，无路可走的原因可能是当下点的四周位置（下面统称为“邻居”）已经全部走过了，即它们已经在栈中了，或者是走到了边角的位置。那么此时无路可走该怎么办呢？是重新从起点开始呢，还是怎样。理论上都可行，不过考虑到效率，即让算法尽量少做重复的事情，我选择在无路可走时，将当下的路线（一个由点序列组成的数组）做记录（存入一个集合中，这个集合记录着所有历史路线），然后回退并将离开的位置从栈弹出，每次回退都将当下路线记录为历史路线，直到周围存在“没有在栈中的点”时不再回退，而是转向新的位置。此时，最近一次回退的那个历史路线决定了下次不会再走这个路线的方向。（假如连续回退了N步，那么最近一次回退的那个历史路线则是临近前N-1次回退历史路线的子集）。不断以上面的方式进行下去，由于“地图”是有限的，当所有可能路线全部遍历过时，最终一定会回到起点。此时历史路线集合列表，记录了从起点达地图上所有点的所有路线。

四、算法描述：

  1、输入：一个二维数组M[26][5]。（第一维度角标1到4分别代表上右下左四个方向，第二维度角标1到25分别代表图的每个点，一次从地图的左上到右下为1到25。数组中的每个值，比如M[20][1]=15 表示地图编号为20的点的上边是编号为15的点，M[20][2]=0表示地图编号为20的点的右方没有通路。其中M[i][0]=0,M[0][j]=0）

  2、初始化：定义栈Q = {1} 和 集合H = {} .（Q中记录了当下路径中依次走过的所有点，H记录着所有的历史路径。）

  3、重复以下动作，直到 Q = {}：

  根据Q的栈顶元素d，和邻接表M找出d的所有临近点元素，从其中随机选择一个元素，且Q中不存在该元素，若找到，将该元素放入Q中。若找不到，则将Q的副本存入H中，并将d从Q中弹出。

  4、输出：H。

五、算法实现

  到这里，对原始问题的抽象思考过程和算法的理论分析过程已经描述完毕。下面就是用实际的代码实现该算法并做到可视化。如果不考虑可视化，那么随便一个编程语言都可以很方便的实现它，我之前用java写过，将结果输出在控制台那种。不过感觉没啥意思，还是想要可视化的感觉。当时很长一段时间我都不知道如何将它可视化，直到我遇到了React，深入了解后，发现用React来完成该算法的可视化，真是再合适不过了。

  由于React是面向组件开发的模式，并且可以很容易根据状态来自动渲染页面，所以可视化部分的设计，就变成对原始“地图”的拆解和状态的定义。我设计的最基础的组件和整体样式如下图这样：

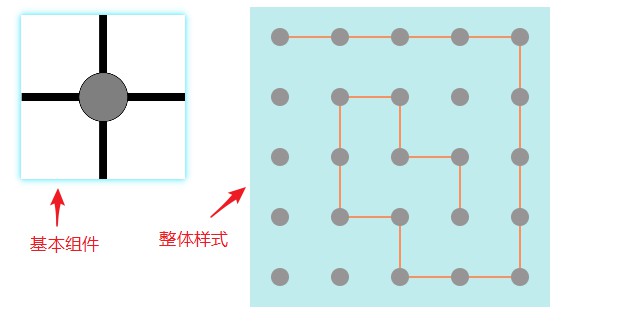
  每个位置（点）都有上下左右四个方向，点与点之间，如果存在连线，则将对应方向的线条用CSS渲染成“block”，其他渲染成“none”.这个过程在定义好CSS样式后，根据数据状态，React会自动帮助界面渲染，不需要反复用js写渲染逻辑。

  最终效果请点击这个 程序链接1 或程序链接2 查看。以下附带部分代码。另外关于实现过程中对性能的优化，我已经做了一些努力，以后也会不断对其优化，欢迎有兴趣的朋友提出高见。

  1. import React, { Component } from 'react';
  2. import './AppDemo.css';
  3. import Grid from './Grid';
  5. class AppDemo extends Component {
  6.     constructor(proprs) {
  7.         super(proprs);
  8.         var width = 5;
  9.         var height = 5;
  10.         var matrix = this.init(width,height);
  11.         var x = 50;
  12.         var start = Math.floor(Math.random() * width * height + 1);
  13.         this.state = {
  14.             matrix: matrix,
  15.             start: start,
  16.             arr: [start],
  17.             historyPath: [],
  18.             width: width,
  19.             height: height,
  20.             timeID: 0,
  21.             speed: 5,
  22.             random: true,
  23.             x: x,
  24.             time: 0
  25.         }
  26.     }
  27.     init(width,height){
  28.         var matrix = [[0, 1, 2, 3, 4]];
  29.         for (var numb = 1; numb <= width * height; numb++) {
  30.             var up = numb > width ? numb - width : 0;
  31.             var right = (numb % width) !== 0 ? numb + 1 : 0;
  32.             var down = numb <= width * (height - 1) ? numb + width : 0;
  33.             var left = ((numb - 1) % width) !== 0 ? numb - 1 : 0;
  34.             var arr = [numb];
  35.             arr.push(up);
  36.             arr.push(right);
  37.             arr.push(down);
  38.             arr.push(left);
  39.             matrix.push(arr);
  40.         }
  41.         return matrix;
  42.     }
  43.     handle() {
  44.         //var beginTime1=0;
  45.         //var beginTime2=0;
  46.         //beginTime1 = new Date().getTime();
  47.         var nowRow = this.state.arr[this.state.arr.length - 1];//获取当下的位置编号
  48.         var arr = this.state.arr;//路径编号
  49.         var matrix = this.state.matrix;//矩阵存储结构
  50.         var historyPath = this.state.historyPath;//历史路径
  51.         if (arr.length > 0) {//如果路径长度>0
  52.             var next = false;//默认找不到路径
  53.             var ran = 1
  54.             if (this.state.random) {
  55.                 ran = Math.floor(Math.random() * 4 + 1);
  56.             }
  57.             //var beginTime4 = new Date().getTime();
  58.             for (var i = 0; i < 4; i++) {
  59.                 var nextNumb = matrix[nowRow][ran];
  60.                 if (nextNumb !== 0 && !this.containNowPath(nextNumb)) {//找到路径
  61.                     arr.push(nextNumb);//将新元素入栈
  62.                     if (!this.containHistoryPath(arr)) {//若新路径没有在历史路径中出现过，则走该路径
  63.                         this.setState({
  64.                             arr: arr
  65.                         });
  66.                         next = true;
  67.                         break;
  68.                     } else {//若新路径在历史路径中出现过，则跳过该路径
  69.                         arr.pop();//放弃该位置
  70.                         ran = ran + 1 > 4 ? 1 : ran + 1;
  71.                     }
  72.                 } else {
  73.                     ran = ran + 1 > 4 ? 1 : ran + 1;
  74.                 }
  75.             }
  77.             //var beginTime5 = new Date().getTime();
  78.             if (!next) {//如果无路可走
  79.                 //判断当下路径（未退步之前）是否包含于历史记录。
  80.                 if (!this.containHistoryPath(arr)) {
  81.                     historyPath.push(arr.slice());//若没有包含与历史中，则将新的尝试路径保存进历史路径集中
  82.                 }
  83.                 arr.pop();//将最后一个元素弹出，相当于后退一步
  84.                 this.setState({//修改当前改变了的状态
  85.                     arr: arr,
  86.                     historyPath: historyPath
  87.                 });
  88.             }
  89.         } else {//若路径遍历结束，则换一个起点继续遍历。
  90.             this.stop();
  91.             // this.setState({
  92.             //     start: this.state.start + 1,
  93.             //     arr: [this.state.start + 1],
  94.             //     historyPath: [],
  95.             //     len: 5
  96.             // });
  97.         }
  98.         // beginTime2 = new Date().getTime();
  99.         // var time = beginTime2 - beginTime1 ;
  100.         // if(time> this.state.time){
  101.         //     this.setState({//修改当前改变了的状态
  102.         //         time: time
  103.         //     });
  104.         // }
  105.         //alert(time);
  106.     }
  108.     containNowPath(row) {//判断下一个位置是否已经存在当下路径中。
  109.         var r = false;
  110.         for (var i = 0; i < this.state.arr.length; i++) {
  111.             r = this.state.arr[i] === row;
  112.             if (r) {
  113.                 break;
  114.             }
  115.         }
  116.         return r;
  117.     }
  118.     containHistoryPath(arr) {//从历史路径中查找是否已经存在下一步要走的路径
  119.         var r = false;
  120.         var historyPath = this.state.historyPath;
  121.         for (var i = historyPath.length - 1; i >= 0; i--) {
  122.             r = historyPath[i].toString().indexOf(arr.toString()) !== -1;
  123.             if (r) {
  124.                 break;
  125.             }
  126.         }
  127.         return r;
  128.     }
  129.     render() {
  130.         return (
  131.             <div>
  132.                 <div style={{ margin: "50px auto 0px auto", width: (this.state.width * this.state.x) + "px", minWidth: "700px" }}>
  133.                     <div className="control">
  134.                         <button type="button" onClick={() => this.start()}>开始</button>
  135.                         <button type="button" onClick={() => this.stop()}>暂停</button>
  136.                         <button type="button" onClick={() => this.start()}>继续</button>
  137.                         <button type="button" onClick={() => this.step()}>单步</button>
  138.                         <apan style={{ margin: "0px auto 0px 10px", width: "120px", display: "inline-block" }}>尝试次数：{this.state.historyPath.length}</apan>
  139.                         <apan style={{ margin: "0px auto 0px 10px" }}>速度：</apan>
  140.                         <button style={this.state.speed === 1000 ? { backgroundColor: "#61dafb" } : {}} type="button" onClick={() => this.speed(1000)}>极慢</button>
  141.                         <button style={this.state.speed === 500 ? { backgroundColor: "#61dafb" } : {}} type="button" onClick={() => this.speed(500)}>慢</button>
  142.                         <button style={this.state.speed === 100 ? { backgroundColor: "#61dafb" } : {}} type="button" onClick={() => this.speed(100)}>中</button>
  143.                         <button style={this.state.speed === 50 ? { backgroundColor: "#61dafb" } : {}} type="button" onClick={() => this.speed(50)}>快</button>
  144.                         <button style={this.state.speed === 5 ? { backgroundColor: "#61dafb" } : {}} type="button" onClick={() => this.speed(5)}>极快</button>
  145.                         <apan style={{ margin: "0px auto 0px 10px", width: "50px", display: "inline-block" }}></apan>
  146.                         <button style={this.state.random ? { backgroundColor: "#61dafb" } : {}} type="button" onClick={() => this.random()}>随机</button><br />
  147.                     </div>
  148.                     <div className="control2">
  149.                         <button style={{ width: "80px" }} type="button" onClick={() => this.addheight(1)}>增加行+</button>
  150.                         <button style={{ width: "80px" }} type="button" onClick={() => this.addwidth(1)}>增加列+</button>
  151.                         <button style={{ width: "80px" }} type="button" onClick={() => this.big(1)}>放大+</button><br />
  152.                         <button style={{ width: "80px" }} type="button" onClick={() => this.addheight(-1)}>减少行-</button>
  153.                         <button style={{ width: "80px" }} type="button" onClick={() => this.addwidth(-1)}>减少列-</button>
  154.                         <button style={{ width: "80px" }} type="button" onClick={() => this.big(-1)}>缩小-</button>
  155.                     </div>
  156.                     <Grid x={this.state.x} width={this.state.width} height={this.state.height} arr={this.state.arr} />
  158.                 </div>
  159.             </div >
  161.         )
  162.     }
  163.     addwidth(n) {
  164.         this.stop();
  165.         var width = this.state.width;
  166.         width = width + n;
  167.         if (width > 0 && width * this.state.x <= 1000) {
  168.             var matrix = this.init(width,this.state.height);
  169.             var start = Math.floor(Math.random() * width * this.state.height + 1);
  170.             this.setState({
  171.                 matrix : matrix,
  172.                 start: start,
  173.                 arr: [start],
  174.                 historyPath: [],
  175.                 width: width
  176.             });
  177.         } else {
  178.             this.setState({
  179.                 width: Math.floor(1000 / this.state.x),
  180.             });
  181.         }
  182.     }
  183.     addheight(n) {
  184.         this.stop();
  185.         var height = this.state.height;
  186.         height = height + n;
  187.         if (height > 0 && height * this.state.x <= 500) {
  188.             var matrix = this.init(this.state.width,height);
  189.             var start = Math.floor(Math.random() * this.state.width * height + 1);
  190.             this.setState({
  191.                 matrix:matrix,
  192.                 start: start,
  193.                 arr: [start],
  194.                 historyPath: [],
  195.                 height: height
  196.             });
  197.         } else {
  198.             this.setState({
  199.                 height: Math.floor(500 / this.state.x),
  200.             });
  201.         }
  202.     }
  203.     big(n) {
  204.         var x = this.state.x;
  205.         x = x + n;
  206.         if (x > 0 && ((x * this.state.width <= 1000) || (x*this.state.height<=500)) ){
  207.             this.setState({
  208.                 x: x
  209.             });
  210.         } else {
  211.             this.setState({
  212.                 x: Math.floor(x * this.state.width > x*this.state.height?1000/this.state.width:500/this.state.height)
  213.             });
  214.         }
  215.     }
  216.     // shouldComponentUpdate(nextProps, nextState){
  217.     //     return nextState.arr.length>100;
  218.     // }
  219.     step() {
  220.         this.stop();
  221.         this.handle();
  222.     }
  223.     start() {
  224.         var timeID = this.state.timeID;
  225.         if (timeID === 0) {
  226.             timeID = setInterval(
  227.                 () => this.handle(),
  228.                 this.state.speed
  229.             );
  230.         }
  231.         this.setState({
  232.             timeID: timeID
  233.         });
  234.     }
  235.     stop() {
  236.         var timeID = this.state.timeID;
  237.         if (timeID !== 0) {
  238.             clearInterval(timeID);
  239.         }
  240.         this.setState({
  241.             timeID: 0
  242.         });
  243.     }
  244.     componentDidMount() {
  245.         var matrix = [[0, 1, 2, 3, 4]];
  246.         var width = this.state.width;
  247.         var height = this.state.height;
  248.         for (var numb = 1; numb <= width * height; numb++) {
  249.             var up = numb > width ? numb - width : 0;
  250.             var right = (numb % width) !== 0 ? numb + 1 : 0;
  251.             var down = numb <= width * (height - 1) ? numb + width : 0;
  252.             var left = ((numb - 1) % width) !== 0 ? numb - 1 : 0;
  253.             var arr = [numb];
  254.             arr.push(up);
  255.             arr.push(right);
  256.             arr.push(down);
  257.             arr.push(left);
  258.             matrix.push(arr);
  259.         }
  260.     }
  261.     speed(n) {
  262.         var timeID = this.state.timeID;
  263.         clearInterval(timeID);
  264.         timeID = 0;
  265.         timeID = setInterval(
  266.             () => this.handle(),
  267.             n
  268.         );
  269.         this.setState({
  270.             timeID: timeID,
  271.             speed: n
  272.         });
  273.     }
  274.     random() {
  275.         this.setState({
  276.             random: !this.state.random
  277.         });
  278.     }
  280.     sleep(numberMillis) {
  281.         var now = new Date();
  282.         var exitTime = now.getTime() + numberMillis;
  283.         while (true) {
  284.             now = new Date();
  285.             if (now.getTime() > exitTime)
  286.                 return true;
  287.         }
  288.     }
  289. }
  291. export default AppDemo;

5 X 5 方阵引出的寻路算法 之 路径遍历（完结）的更多相关文章

  1. JS算法之A*（A星）寻路算法

    今天写一个连连看的游戏的时候,接触到了一些寻路算法,我就大概讲讲其中的A*算法. 这个是我学习后的一点个人理解,有错误欢迎各位看官指正. 寻路模式主要有三种:广度游戏搜索.深度优先搜索和启发式搜索. ...

  2. 寻路算法之A*算法详解

    前言 在实际开发中我们会经常用到寻路算法,例如MMOARPG游戏魔兽中,里面的人物行走为了模仿真实人物行走的体验,会选择最近路线达到目的地,期间会避开高山或者湖水,绕过箱子或者树林,直到走到你所选定的 ...

  3. A星寻路算法介绍

    你是否在做一款游戏的时候想创造一些怪兽或者游戏主角,让它们移动到特定的位置,避开墙壁和障碍物呢? 如果是的话,请看这篇教程,我们会展示如何使用A星寻路算法来实现它! 在网上已经有很多篇关于A星寻路算法 ...

  4. A*寻路算法探究

    A*寻路算法探究 A*算法常用在游戏的寻路,是一种静态网路中求解最短路径的搜索方法,也是解决很多搜索问题的算法.相对于Dijkstra,BFS这些算法在复杂的搜索更有效率.本文在U3D中进行代码的测试 ...

  5. A*寻路算法

    对于初学者而言,A*寻路已经是个比较复杂的算法了,为了便于理解,本文降低了A*算法的难度,规定只能横竖(四方向)寻路,而无法直接走对角线,使得整个算法更好理解. 简而言之,A*寻路就是计算从起点经过该 ...

  6. 算法：Astar寻路算法改进，双向A*寻路算法

    早前写了一篇关于A*算法的文章:<算法:Astar寻路算法改进> 最近在写个js的UI框架,顺便实现了一个js版本的A*算法,与之前不同的是,该A*算法是个双向A*. 双向A*有什么好处呢 ...

  7. 算法：Astar寻路算法改进

    早前写了一篇<RCP:gef智能寻路算法(A star)> 出现了一点问题. 在AStar算法中,默认寻路起点和终点都是N x N的方格,但如果用在路由上,就会出现问题. 如果,需要连线的 ...

  8. js实现A*寻路算法

    这两天在做百度前端技术学院的题目,其中有涉及到寻路相关的,于是就找来相关博客进行阅读. 看了Create Chen写的理解A*寻路算法具体过程之后,我很快就理解A*算法的原理.不得不说作者写的很好,通 ...

  9. 用简单直白的方式讲解A星寻路算法原理

    很多游戏特别是rts,rpg类游戏,都需要用到寻路.寻路算法有深度优先搜索(DFS),广度优先搜索(BFS),A星算法等,而A星算法是一种具备启发性策略的算法,效率是几种算法中最高的,因此也成为游戏中 ...

随机推荐

  1. Python入门基础(9)__面向对象编程_1

    定义一个只包含方法的类 class 类名: def 方法1(self,参数列表): pass def 方法2(self,参数列表): pass 当一个类定义之后,要使用这个类来创键对象.语法如下: 对 ...

  2. 洛谷P4995 跳跳！题解

    求关注,求赞,求评论QAQ 题目:https://www.luogu.org/problemnew/show/P4995 简单描述一下吧,就是说有n块石头,起始可以跳到任何一块上面,接着也是,只不过每 ...

  3. [leetcode]375 Guess Number Higher or Lower II (Medium)

    原题 思路: miniMax+DP dp[i][j]保存在i到j范围内,猜中这个数字需要花费的最少 money. "至少需要的花费",就要我们 "做最坏的打算,尽最大的努 ...

  4. python递归-三元表达式-列表生成式-字典生成式-匿名函数-部分内置函数-04

    递归 递归: # 函数在调用阶段直接或间接地又调用了自身 应用场景: # 将列表中的数字依次打印出来(循环的层数是你必须要考虑的点)   -->  l = [1, [2, [3, [4, [5, ...

  5. mongodb的索引原理

    首先说一下为什么要有索引,大家都知道mongdb是非关系型文档类型数据库,用过的人都有同一种感受,查询的效率太低,当你想提高查询效率的时候可以就需要使用索引了. 哈哈,本来想写一篇的,在网上看到了一篇 ...

  6. 装饰器和"开放-封闭"原则

    装饰器和"开放-封闭"原则 "开放-封闭"原则 软件开发中的"开放-封闭"原则,它规定已经实现的功能代码不应该被修改,但可以被扩展,即: 封 ...

  7. js - 原生ajax访问后台读取数据并显示在页面上

    1.前台调用ajax访问后台方法,并接收数据 <%@ page contentType="text/html;charset=UTF-8" language="ja ...

  8. WebGL着色器32位浮点数精度损失问题

    问题 WebGL浮点数精度最大的问题是就是因为js是64位精度的,js往着色器里面穿的时候只能是32位浮点数,有效数是8位,精度丢失比较严重. 这篇文章里讲了一些处理方式,但是视坐标这种方式放在我们的 ...

  9. 计算机原理以及PythonIDE配置和使用

    计算机基础 在巩固了昨日学习知识的基础上,增加了新的内容 整个关于计算机基础的学习可以浓缩为五个问题 什么是编程? 人与计算机之间的交互操作,使人可以奴役计算机从而让其代替人类工作的行为 操作系统有什 ...

  10. SQL语句中的as