Katu Puzzle（POJ3678+2-SAT问题+tarjan缩点）

题目链接：http://poj.org/problem?id=3678

题目：

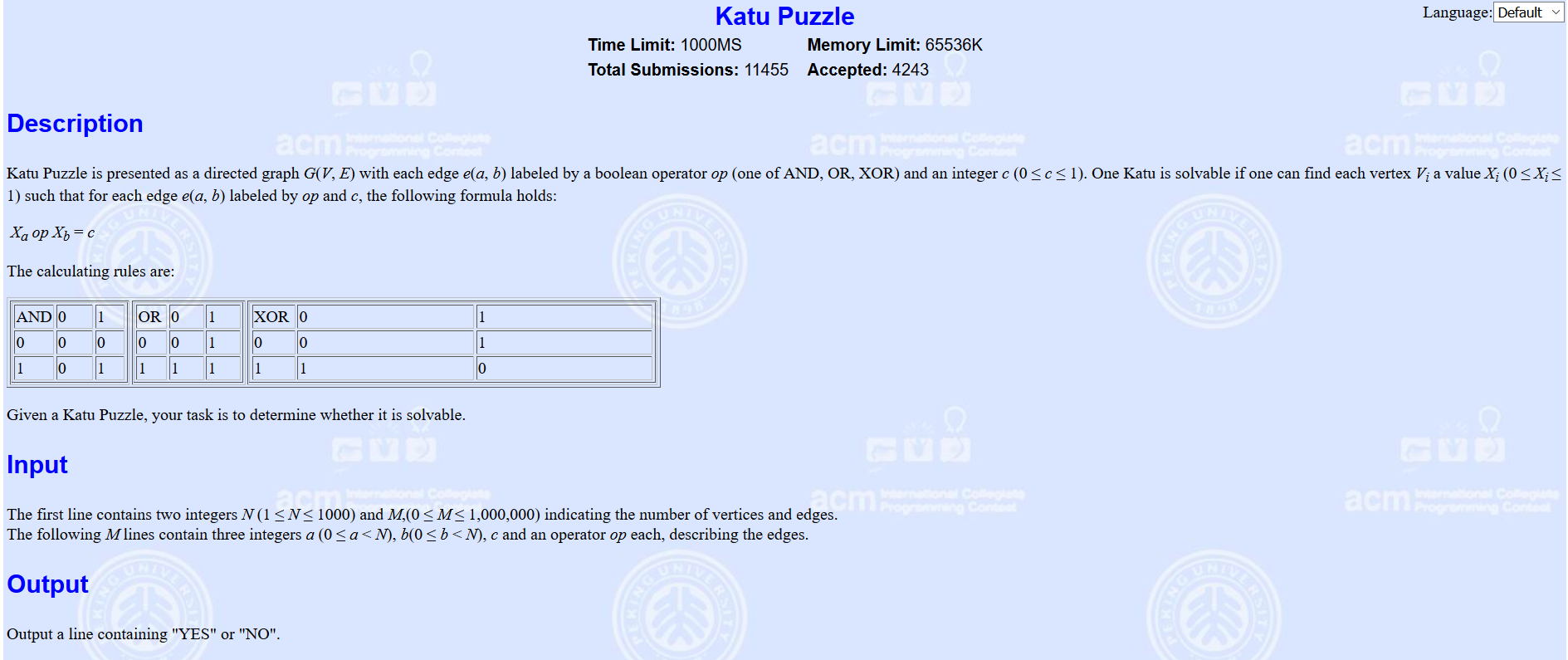
题意：给你a,b,c,op，op为逻辑运算符或、与、异或，使得a op b = c，让你判断这些运算符是否存在矛盾，不存在输出YES，存在输出NO。

思路：2-SAT问题。2-SAT问题一般都是每个节点有两种选择，并且在节点中间将存在一定的限制，譬如a为1，那么b必须为1或a为0，b必须为1……而且当一个命题存在时，它的逆否命题必然存在（此处由命题为真，则其逆否命题也为真得证）。我们通过将这些关系转换成有向的边，通过tarjan缩点，我们可以通过判断同一个节点是否它的两种选择在同一个SCC中来决定是否存在矛盾。此题我们假设i为i节点取1，i+n为i节点取0，然后对c和op进行分类讨论，进行建图跑tarjan，从而解决此题。

代码实现如下：

 #include <set>
 #include <map>
 #include <queue>
 #include <stack>
 #include <cmath>
 #include <bitset>
 #include <cstdio>
 #include <string>
 #include <vector>
 #include <cstdlib>
 #include <cstring>
 #include <iostream>
 #include <algorithm>
 using namespace std;

 typedef long long ll;
 typedef pair<ll, ll> pll;
 typedef pair<ll, int> pli;
 typedef pair<int, ll> pil;;
 typedef pair<int, int> pii;
 typedef unsigned long long ull;

 #define lson i<<1
 #define rson i<<1|1
 #define bug printf("*********\n");
 #define FIN freopen("D://code//in.txt", "r", stdin);
 #define debug(x) cout<<"["<<x<<"]" <<endl;
 #define IO ios::sync_with_stdio(false),cin.tie(0);

 const double eps = 1e-;
 const int mod = ;
 const int maxn = 1e6 + ;
 const double pi = acos(-);
 const int inf = 0x3f3f3f3f;
 const ll INF = 0x3f3f3f3f3f3f3f;

 int n, m, a, b, c, tot, cnt, num, top;
 char op[];
 int head[<<];
 int vis[<<], dfn[<<], low[<<], stc[<<], p[<<];

 struct edge {
     int v, next;
 }ed[maxn<<];

 void addedge(int u, int v) {
     ed[tot].v = v;
     ed[tot].next = head[u];
     head[u] = tot++;
 }

 void tarjan(int x) {
     dfn[x] = low[x] = ++num;
     stc[++top] = x, vis[x] = ;
     for(int i = head[x]; ~i; i = ed[i].next) {
         int y = ed[i].v;
         if(!dfn[y]) {
             tarjan(y);
             low[x] = min(low[x], low[y]);
         } else if(vis[y]) {
             low[x] = min(low[x], low[y]);
         }
     }
     if(dfn[x] == low[x]) {
         int y; cnt++;
         do {
             y = stc[top--], vis[y] = ;
             p[y] = cnt;
         } while(x != y);
     }
 }

 int main() {
     //FIN;
     scanf("%d%d", &n, &m);
     memset(head, -, sizeof(head));
     for(int i = ; i <= m; i++) {
         scanf("%d%d%d%s", &a, &b, &c, op);
         if(op[] == 'A') {
             if(c == ) {
                 addedge(a + n, a);
                 addedge(b + n, b);
             } else {
                 addedge(a, b + n);
                 addedge(b, a + n);
             }
         } else if(op[] == 'O') {
             if(c == ) {
                 addedge(a + n, b);
                 addedge(b + n, a);
             } else {
                 addedge(a, a + n);
                 addedge(b, b + n);
             }
         } else {
             if(c == ) {
                 addedge(a, b + n);
                 addedge(b, a + n);
                 addedge(a + n, b);
                 addedge(b + n, a);
             } else {
                 addedge(a, b);
                 addedge(b, a);
                 addedge(a + n, b + n);
                 addedge(b + n, a + n);
             }
         }
     }
     for(int i = ; i <  * n; i++) {
         if(!dfn[i]) {
             tarjan(i);
         }
     }
     int flag = ;
     for(int i = ; i < n; i++) {
         if(p[i] == p[i+n]) {
             flag = ;
             break;
         }
     }
     if(flag) puts("YES");
     else puts("NO");
     return ;
 }