LeetCode65. 有效数字

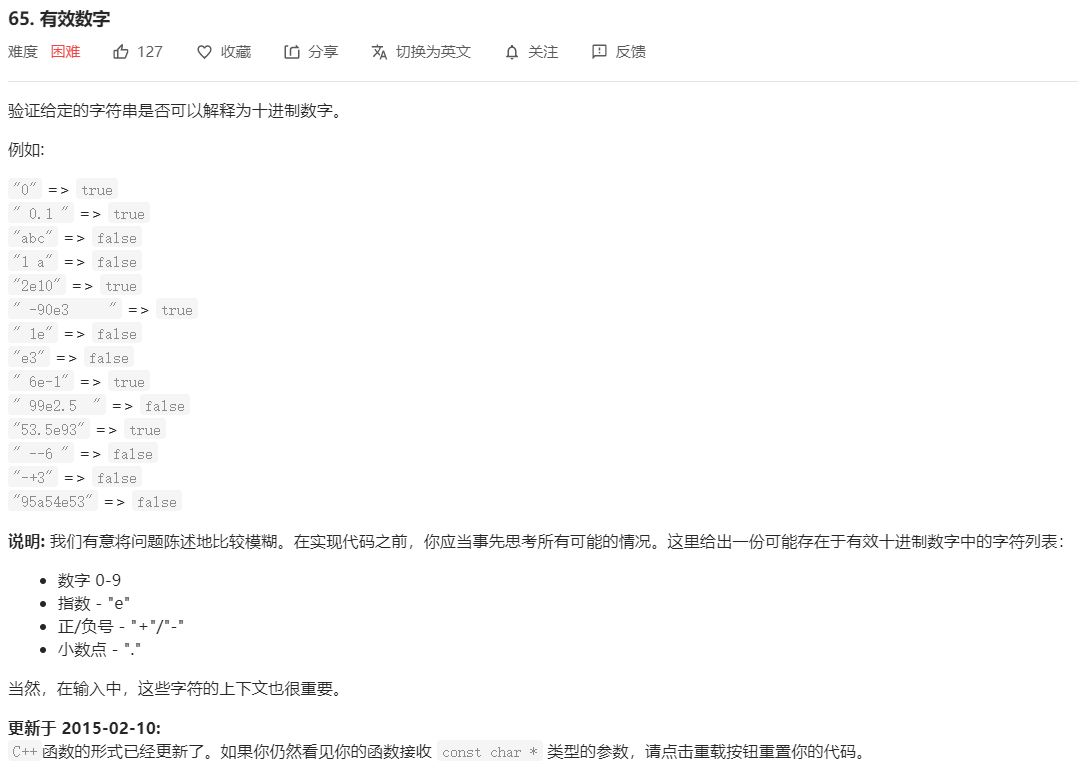
这题完美的诠释了什么叫“面向测试用例编程”。由于要考虑的情况很多，所以基本的思路是先根据给出的测试用例写出规则判断无效的情况，然后再根据提交的错误对剩下的情况进行特判，如果不满足所有“无效的情况”，则有效。题目特别提了“我们有意将问题陈述地比较模糊”，这个“有意地陈述地模糊”就很灵性，所以一开始很难考虑到所有情况，WA几次就知道有哪些测试用例（规则）了。

先从题目给出的测试用例里总结几点规则：

1. 给出的字符串可能会包含前缀和后缀的空格，需要先去掉前缀和后缀的空格；
2. 有可能字符串是一个科学计数法的数字，因此会出现字符'e'或'E'，但'e'（或'E'）只能出现一次，且不能出现在字符串的开头和结尾位置；
3. 'e'（或'E')的后面可能紧跟一个'+'或'-'，正负号只能出现在两个地方，一是字符串开头，二就是'e'(或'E')的后面，其他位置如果出现正负号，就可以判定为无效！ 另外，'e'(或'E')后面如果出现了正负号，后面还必须有数字，所以要判断正负号是不是字符串的结尾，如果是，也可以判定为无效；
4. 字符串开头可以是正负号，但如果只有正负号，则无效；
   
   再从提交的测试用例里总结几点规则：
5. 字符串可以由'.'开头，比如".1"就表示0.1，这种'.'后面是数字的就是合法的，'.'后面跟着其他字符就是非法的；
6. '.'和'e'只能分别出现一次，多于一次就是无效的

class Solution {
public:
    bool isNumber(string s) {
        int left = 0, right = s.size() - 1;                  //分别从左右过滤掉前缀和后缀的空格
        while(left <= right && s[left] == ' ') {
            ++left;
        }
        while(left <= right && s[right] == ' ') {
            --right;
        }
        if(left > right) {                                    //如果字符串只有空格组成，则无效
            return false;
        }
        s = s.substr(left, right - left + 1);                 //留下删除掉前缀和后缀的空格之后的字符串
        if(s[0] == '+' || s[0] == '-') {                      //如果字符串由正负号开头，则删掉开头的字符串再作判断
            s = s.substr(1);                                  //substr只传入一个参数1，表示留下从第一个位置到末尾的子串（即删除第0个位置的正负号）
        }
        if(s.empty()) {                                       //如果删掉正负号之后字符串为空，则无效
            return false;
        }
        if(s[0] == '.' && (s.size() == 1 || s[1] == 'e' || s[1] == 'E')) {    //如果字符串有'.'开头，则有三种情况是无效的：(1)字符串只有一个字符'.'; (2)下一个字符是'e'; (3)下一个字符是'E'。 实际上，只要'.'后面的字符不是数字就都是无效的，只不过其他情况在别处判断了。
            return false;
        }
        int dotNum = 0, eNum = 0;                  //记录'.'和'e'(或'E')的数量
        for(int i = 0; i < s.size(); ++i) {
            if(s[i] == '.') {
                if(dotNum > 0 || eNum > 0) {       //如果'.'出现次数大于1或者'.'在'e'(或'E')之后出现，则无效
                    return false;
                } else {
                    ++dotNum;
                }
            } else if(s[i] == 'e' || s[i] == 'E') {
                if(i == 0 || i == s.size() - 1 || eNum > 0) {      //如果'e'(或'E')出现在开头或者结尾位置，或者出现次数大于1，则无效
                    return false;
                } else if(s[i + 1] == '+' || s[i + 1] == '-') {     //如果'e'(或'E')后面的字符是正负号，需要特判
                    if(i + 1 == s.size() - 1) {                     //正负号后面需要有数字，如果正负号已经是最后一个字符了（后面啥都没），则无效
                        return false;
                    } else {
                        ++i;                                        //如果正负号后面还有东西，我们就跳过正负号，继续判断后面的
                    }
                }
                ++eNum;
            } else if(!(s[i] >= '0' && s[i] <= '9')) {              //其他情况的字符只能是数字，其他都是无效的
                return false;
            }
        }
        return true;                                                //如果不满足上述任何情况，我们就认为字符串可以表示为一个有效的数字！
    }
};

复杂度分析：由于只遍历一遍字符串，时间复杂度是O(n)；只开了常数个变量，空间复杂度是O(1)。