Java实现WUST 1002: 哈夫曼树

[问题描述]

根据给定的若干权值可以构造出一颗哈夫曼树。构造的哈夫曼树可能不唯一，但是按照下面的选取原则所构造出来的哈夫曼树应该是唯一的。

（1）每次选取优先级最低的两个结点，优先级最低的作为左子树，优先级高的作为右子树；

（2）结点优先级大小的比较首先比较它们的权值，权值大的优先级高，权值小的优先级低，权值相等的按照位置关系来比较，位置在前面的优先级低，位置在后面的优先级高。

（3）增加的新结点位置依次往后。

根据你所构造的哈夫曼树来设计每个权值的哈夫曼编码（左子树0右子树1），并计算该哈夫曼树的WPL值。

[输入]

包含多组数据

每组数据包含2行，第一行输入权值个数n（0<n<20）,第2行为顺序输入的n个权值，均为整数（小于100），

[输出]

对于每组数据，输出n+1行，前面n行为每个权值所对应的赫夫曼编码（按照输入顺序给出），第n+1行用来输出你所构造的哈夫曼树的WPL值。

[样例输入]

5

11 4 2 5 7

6

2 3 4 7 8 9

[样例输出]

11

011

010

00

10

64

1110

1111

110

00

01

10

80

PS：

他这个是特别版的哈夫曼树，相同的权值时，位置靠左面的会小，

所以你查询的时候，先靠左查询，其他不懂得在评论

哈夫曼树相关的几个名词

路径：在一棵树中，一个结点到另一个结点之间的通路，称为路径。图 1 中，从根结点到结点 a 之间的通路就是一条路径。

路径长度：在一条路径中，每经过一个结点，路径长度都要加 1 。例如在一棵树中，规定根结点所在层数为1层，那么从根结点到第 i 层结点的路径长度为 i - 1 。图 1 中从根结点到结点 c 的路径长度为 3。

结点的权：给每一个结点赋予一个新的数值，被称为这个结点的权。例如，图 1 中结点 a 的权为 7，结点 b 的权为 5。

结点的带权路径长度：指的是从根结点到该结点之间的路径长度与该结点的权的乘积。例如，图 1 中结点 b 的带权路径长度为 2 * 5 = 10 。

树的带权路径长度为树中所有叶子结点的带权路径长度之和。通常记作 “WPL” 。例如图 1 中所示的这颗树的带权路径长度为：

WPL = 7 * 1 + 5 * 2 + 2 * 3 + 4 * 3

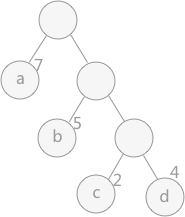
图1 哈夫曼树

什么是哈夫曼树

当用 n 个结点（都做叶子结点且都有各自的权值）试图构建一棵树时，如果构建的这棵树的带权路径长度最小，称这棵树为“最优二叉树”，有时也叫“赫夫曼树”或者“哈夫曼树”。

在构建哈弗曼树时，要使树的带权路径长度最小，只需要遵循一个原则，那就是：权重越大的结点离树根越近。在图 1 中，因为结点 a 的权值最大，所以理应直接作为根结点的孩子结点。

构建哈夫曼树的过程

对于给定的有各自权值的 n 个结点，构建哈夫曼树有一个行之有效的办法：

在 n 个权值中选出两个最小的权值，对应的两个结点组成一个新的二叉树，且新二叉树的根结点的权值为左右孩子权值的和；

在原有的 n 个权值中删除那两个最小的权值，同时将新的权值加入到 n–2 个权值的行列中，以此类推；

重复 1 和 2 ，直到所以的结点构建成了一棵二叉树为止，这棵树就是哈夫曼树。

图 2 哈夫曼树的构建过程

图 2 中，（A）给定了四个结点a，b，c，d，权值分别为7，5，2，4；第一步如（B）所示，找出现有权值中最小的两个，2 和 4 ，相应的结点 c 和 d 构建一个新的二叉树，树根的权值为 2 + 4 = 6，同时将原有权值中的 2 和 4 删掉，将新的权值 6 加入；进入（C），重复之前的步骤。直到（D）中，所有的结点构建成了一个全新的二叉树，这就是哈夫曼树。

import java.util.ArrayList;
import java.util.Collections;
import java.util.Scanner;

public class Demo10哈弗们数 {
	public static class TreeNode implements Comparable<TreeNode>{
		int val;
		boolean bool;
		TreeNode left;
		TreeNode right;

		TreeNode(int x) {
			val = x;
		}

		@Override
		public int compareTo(TreeNode o) {

			// TODO 自动生成的方法存根

			if(this.val>o.val){
				return 1;
			}
			else if(this.val<o.val){
				return -1;
			}
			else {
				if(this.bool){
					return 1;
				}
				else if(o.bool){
					return -1;
				}

			}
			return 0;
		}
	}

	static TreeNode tree = new TreeNode(0);
	static ArrayList<TreeNode> list = new ArrayList<TreeNode>();

	static ArrayList<String> list1 = new ArrayList<String>();

	public static void main(String[] args) {

		Scanner sc = new Scanner(System.in);
		while(sc.hasNext()){
			tree = new TreeNode(0);
			list = new ArrayList<TreeNode>();
			list1 = new ArrayList<String>();
			int sum = 0;

		int n = sc.nextInt();
		int[] num = new int[n];
		for (int i = 0; i < n; i++) {

			num[i] = sc.nextInt();
			TreeNode tree11 = new TreeNode(num[i]);
			list.add(tree11);
		}
		Collections.sort(list);
		// Arrays.sort(num);
		madetree();
		for (int i = 0; i < num.length; i++) {
			findtree(tree, num[i], "");
			System.out.println( list1.get(i));
			sum+=num[i]*list1.get(i).length();

		}
		System.out.println(sum);
	//	System.out.println(list1.size());
		}
	}

	public static void findtree(TreeNode node, int n, String s) {
		if (node.val == n && !node.bool) {
			list1.add(s);
			return;
		}
		if (node.left != null)
			findtree(node.left, n, s + "0");
		if (node.right != null)
			findtree(node.right, n, s + "1");

		return;

	}

	public static void madetree() {
		boolean flag = true;
		while (list.size() != 1) {
			Collections.sort(list);
//			int a = list.get(0);
//			int b = list.get(1);

//			if (a > b) {
//				int temp = a;
//				a = b;
//				b = temp;
//			}
			TreeNode treeleft = list.get(0);
			TreeNode treeright = list.get(1);
			list.remove(0);
			list.remove(0);
			TreeNode treemid = new TreeNode(treeleft.val+treeright.val);
			treemid.left = treeleft;
			treemid.right = treeright;
			treemid.bool = true;
			tree = treemid;
//			if (flag) {
//				flag = false;
//
//				TreeNode treeleft1 = null;
//				TreeNode treeright1 = null;
//
//				if (treemid.val > tree.val) {
//					treeleft1 = tree;
//					treeright1 = treemid;
//
//				} else {
//					treeleft1 = treemid;
//					treeright1 = tree;
//				}
//				TreeNode treemid1 = new TreeNode(tree.val + treemid.val);
//				treemid1.left = treeleft1;
//				treemid1.right = treeright1;
//				treemid1.bool = true;
//				if (tree.val != 0) {
//					tree = treemid1;
//				} else {
//					tree = treemid;
//				}
//			}

			list.add(tree);
		}
	}

}