算法竞赛进阶指南0x33同余

定义

如果整数a，b除以正整数m的余数相同，那么a，b模m同余 。

知识点

拓展欧几里得算法

代码

#include <bits/stdc++.h>
using namespace std;
int exgcd(int a, int b, int &x, int &y)
{
    if(b==0)
    {
        x = 1;
        y = 0;
        return a;
    }
    int d = exgcd(b, a%b, x, y);//代表答案
    int z = x;
    x = y;
    y = z-(a/b)*y;
    return d;
}
int main()
{
    int a, b;
    cin >> a >> b;
    int x, y;
    int ans = exgcd(a, b, x, y);
    printf("%d %d %d", ans, x, y);
    return 0;
}

AcWing97. 约数之和

一看：显然不能使用暴力。

一提到数论，应该下意识想起分解质因数。

#include <bits/stdc++.h>
using namespace std;
const int mod = 9901;
int p[50];
int c[50];
int cnt = 0;//指示总共有多少个素数
void devide(int n)
{
    for(int i = 2; (long long)i*i <= n; i++)
    {
        if(n % i == 0)
        {
            p[++cnt] = i;
            c[cnt] = 0;
            while(n % i==0)
            {
                c[cnt]++;
                n /= i;
            }
        }
    }
    if(n > 1)
    {
        p[++cnt] = n;
        c[cnt] = 1;
    }
}
int ksm(int a, int b, int pp)
{
    int ans = 1 % pp;
    int tmp = a % pp;
    while(b)
    {
        if(b&1) ans = (long long)ans * tmp % pp;
        tmp = (long long)tmp * tmp % pp;
        b  >>= 1;
    }
    return ans%pp;
}
int cal(int i)
{
    int ans = 1;
    int pri = p[i];
    int num = c[i];
    if((pri-1) % mod == 0)
    {
        return (num+1)% mod;
    }

    int fenzi = (ksm(pri, num+1, mod)+mod-1)%mod;
    if((pri-1) % mod != 0)
    {
        int niyuan = ksm(pri-1, mod-2, mod);
        fenzi = (long long)fenzi * niyuan % mod;
    }
    return fenzi;
}
int main()
{
    int ans = 1;
    int A, B;
    cin >> A >> B;
    if(A == 0) //注意需要进行特殊判断
    {
        printf("0");
        return 0;
    }
    devide(A);
    for(int i = 1; i <= cnt; i++)
    {
        c[i] = B * c[i];
    }
    for(int i = 1; i <= cnt; i++)
    {
        int res = cal(i);
        ans = (long long)res * ans % mod; 

    }
    cout << ans;
    return 0;
}

---

AcWing203. 同余方程

AcWing204. 表达整数的奇怪方式

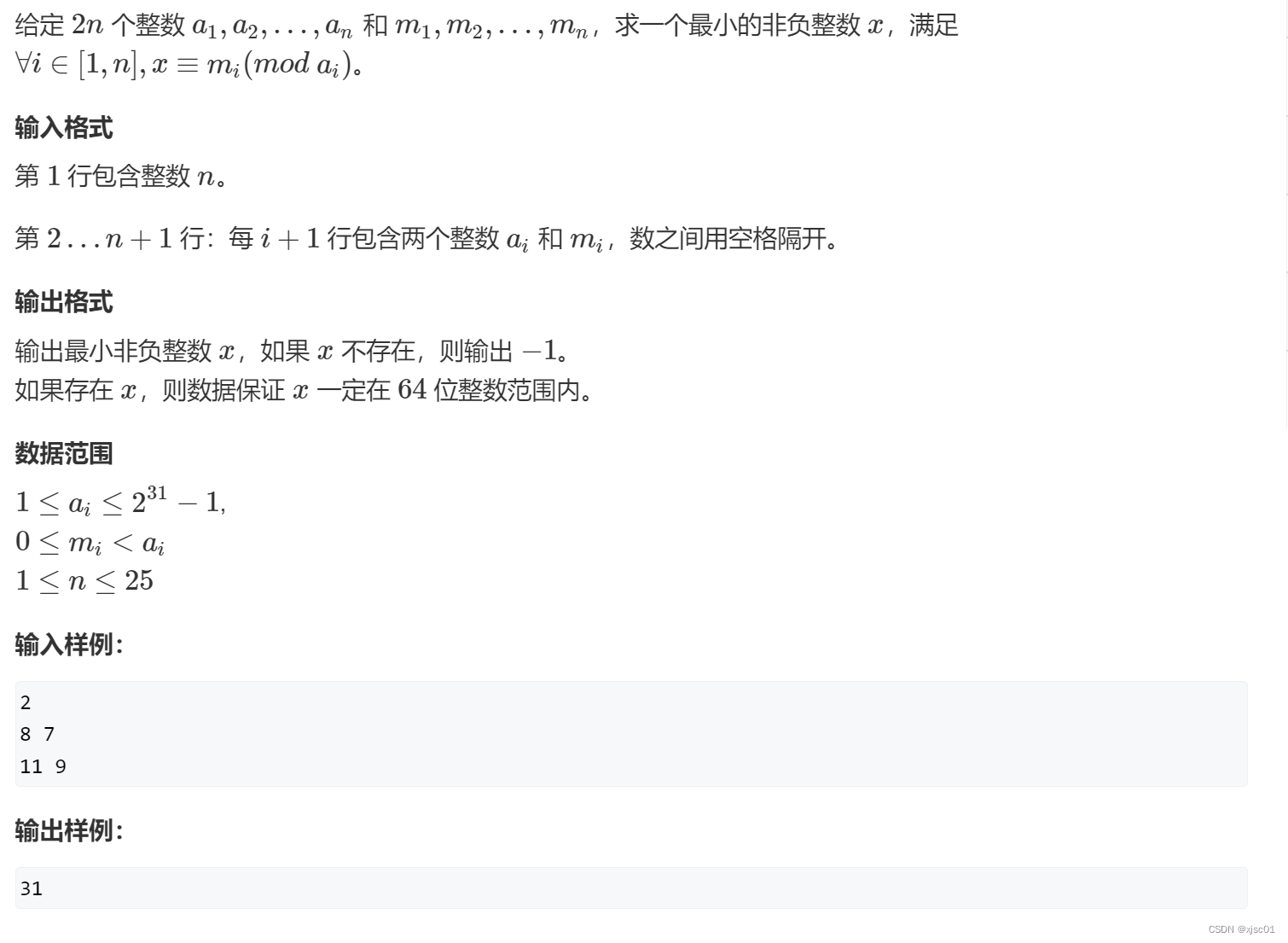
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll exgcd(ll a, ll b, ll &x, ll &y)
{
    if(b==0)
    {
        x = 1;
        y = 0;
        return a;
    }
    ll d = exgcd(b, a%b, x, y);
    ll z = x;
    x = y;
    y = z-(a/b)*y;
    return d;
}
int main()
{
    int n;
    cin >> n;//由于每一个值都是从之前递推得来的，所以我特殊构造第一个值
    ll ans = 0;
    ll lcm = 0;
    ll a, m;
    scanf("%lld%lld", &m, &a);
    ans = a;
    lcm = m;
    n--;
    bool flag = true;
    while(n--)
    {
        ll x, y;
        scanf("%lld%lld", &m, &a);
        ll d = exgcd(lcm, m, x, y);
        a = (a - ans%m + m)%m;
        if(a%d!=0)
        {
            flag = false;
            break;
        }//注意：x并不是同余方程的解（还要算一下比例）
        ll k = x*(a/d)%m;
        //ans += k*lcm;
        //x = (x%m+m)%m;ll k = x*(a/d)%m;
        ans += k*lcm;
        //ans += x*lcm;
        lcm = lcm/d*m;////必须在更新完成lcm之后才可以进行
        ans = (ans%lcm+lcm)%lcm;
    }
    if(flag)
    {
        printf("%lld", ans);
    }
    else
    {
        printf("-1");
    }
    return 0;
}