洛谷P2178 [NOI2015]品酒大会 后缀数组＋单调栈

P2178 [NOI2015]品酒大会

题目链接

https://www.luogu.org/problemnew/show/P2178

题目描述

一年一度的“幻影阁夏日品酒大会”隆重开幕了。大会包含品尝和趣味挑战 两个环节，分别向优胜者颁发“首席品酒家”和“首席猎手”两个奖项，吸引了众多品酒师参加。

在大会的晚餐上，调酒师 Rainbow 调制了 n 杯鸡尾酒。这 n 杯鸡尾酒排成一行，其中第 n 杯酒 (\(1 ≤ i ≤ n\)) 被贴上了一个标签 \(s_i\) ，每个标签都是 26个小写 英文字母之一。设$ str(l, r)$表示第 l 杯酒到第 r 杯酒的 r - l + 1个标签顺次连接构成的字符串。若 \(str(p,p_0)=str(q,q_0)\)，其中 \(1 ≤ p ≤ p_0 ≤ n,1 ≤ q ≤ q_0≤ n, p ≠ q，p_0-p+1 = q_0 - q + 1 = r\)，则称第 p 杯酒与第 q 杯酒是“ r 相似” 的。当然两杯“ r 相似”(\(r > 1\))的酒同时也是“ 1 相似”、“ 2相似”、……、“ (r - 1) 相似”的。特别地，对于任意的 \(1 ≤ p ,q ≤ n,p ≠ q\)，第 p杯酒和第 q 杯酒都 是“ 0 相似”的。

在品尝环节上，品酒师 Freda 轻松地评定了每一杯酒的美味度，凭借其专业的水准和经验成功夺取了“首席品酒家”的称号，其中第 i杯酒 (1 ≤ i ≤ n) 的 美味度为 a_i。现在 Rainbow 公布了挑战环节的问题：本次大会调制的鸡尾酒有一个特点，如果把第 p 杯酒与第 q 杯酒调兑在一起，将得到一杯美味度为 $a_p\times a_q $的 酒。现在请各位品酒师分别对于 r = 0,1,2,⋯,n-1 ，统计出有多少种方法可以 选出 2 杯“ r 相似”的酒，并回答选择 2 杯“r 相似”的酒调兑可以得到的美味度的最大值。

输入输出格式

输入格式：

第 1 行包含 111 个正整数 n ，表示鸡尾酒的杯数。

第 2 行包含一个长度为 n的字符串 S，其中第 i 个字符表示第 i 杯酒的标签。

第 3 行包含 n 个整数，相邻整数之间用单个空格隔开，其中第 i 个整数表示第 i 杯酒的美味度 a_i 。

输出格式：

包括 nnn 行。

第 i 行输出 2 个整数，中间用单个空格隔开。第 111 个整 数表示选出两杯“ (i - 1)相似”的酒的方案数，第 2 个整数表示选出两杯 “ (i−1) 相似”的酒调兑可以得到的最大美味度。若不存在两杯“ (i - 1) 相似” 的酒，这两个数均为 0 。

输入输出样例

输入样例#1：

10

ponoiiipoi

2 1 4 7 4 8 3 6 4 7

输出样例#1：

45 56

10 56

3 32

0 0

0 0

0 0

0 0

0 0

0 0

0 0

输入样例#2：

12

abaabaabaaba

1 -2 3 -4 5 -6 7 -8 9 -10 11 -12

输出样例#2：

66 120

34 120

15 55

12 40

9 27

7 16

5 7

3 -4

2 -4

1 -4

0 0

0 0

说明

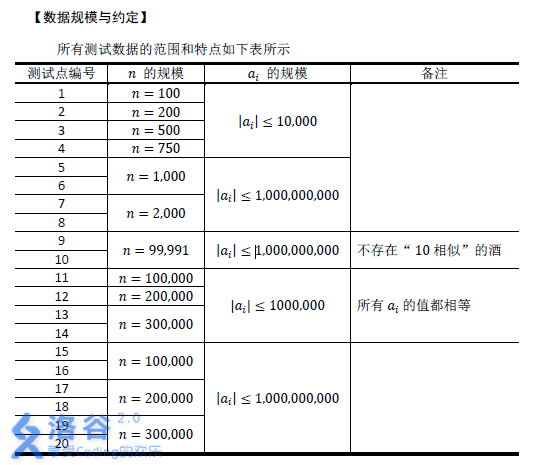
【时限1s，内存512M】

题意

给你一个字符串，任意两个后缀的相似度为0到LCP，求相似度为0～n-1的方案数。对于相似度k,如果第i位和第j位的LCP>=k,那么k相似度方案加一。 并且每个位置i，还有一个权值a[i],对于每个k相似度求最大的a[i] * a[j]（i和j如上所述）

题解

其实已经做过一遍了，但是依然调了好久，真是悲伤。

其实思想并不是很难，我们先打个后缀数组板子，然后考虑height数组。我们以前怎么找后缀i和后缀j的lcp,不就是求他们在height数组之间的最小值吗。那么考虑对于height数组每个位置i的贡献，自然就是找左边第一个小于它的位置记作L[i],同样找到右边R[i],那么只要两个后缀x,y满足\(L[i]\leq x<i\leq y<R[i]\),那么x,y的lcp就是height[i],这样sum[height[i]]+=(R[i]-i)*(i-L[i]), max的求法也是类似的。

这个用单调站栈很好做，但是细节确实需要注意一下。

好久没打后缀数组了，memset(c,0,sizeof(int)*(m+1)) 少写了＋１，

一开始INF定义为123456789,后来才知道原来\(10^9>123456789\),调了半天，真是菜的真实。

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define INF 0x7f7f7f7f
#define N 600050
ll lmx[N],rmx[N],lmi[N],rmi[N],L[N],R[N],sum[N],mx[N],w[N];
int sk[N];
template<typename T>void read(T&x)
{
    ll k=0; char c=getchar();
    x=0;
    while(!isdigit(c)&&c!=EOF)k^=c=='-',c=getchar();
    if (c==EOF)exit(0);
    while(isdigit(c))x=x*10+c-'0',c=getchar();
    x=k?-x:x;
}
void read_char(char &c)
{while(!isalpha(c=getchar())&&c!=EOF);}
struct SuffixArray
{
    char s[N];
    int c[N],t1[N<<1],t2[N<<1],kth[N],rk[N],he[N],n;
    int *x=t1,*y=t2;
    void BuildKth()
    {
        int m=300;
        memset(c,0,sizeof(int)*(m+1));
        for(int i=1;i<=n;i++)c[x[i]=s[i]]++;
        for(int i=1;i<=m;i++)c[i]+=c[i-1];
        for(int i=n;i>=1;i--)kth[c[x[i]]--]=i;
        for(int k=1;k<=n;k<<=1)
        {
            memset(c,0,sizeof(int)*(m+1));
            int p=0;
            for(int i=n-k+1;i<=n;i++)y[++p]=i;
            for(int i=1;i<=n;i++)if (kth[i]-k>0)y[++p]=kth[i]-k;
            for(int i=1;i<=n;i++)c[x[y[i]]]++;
            for(int i=1;i<=m;i++)c[i]+=c[i-1];
            for(int i=n;i>=1;i--)kth[c[x[y[i]]]--]=y[i];
            swap(x,y);
            x[kth[1]]=p=1;
            for(int i=2;i<=n;i++)
                x[kth[i]]=y[kth[i]]==y[kth[i-1]]&&y[kth[i]+k]==y[kth[i-1]+k]?p:++p;
            m=p;
            if (m==n)break;
        }
    }
    void GetHeight()
    {
        for(int i=1;i<=n;i++)rk[kth[i]]=i;
        int k=0;
        for(int i=1;i<=n;i++)
        {
            int j=kth[rk[i]-1];
            if (k)k--;
            while(s[i+k]==s[j+k])k++;
            he[rk[i]]=k;
        }
    }
    void solve()
    {
        int top=0;
        he[n+1]=-1;
        he[1]=-1;
        for(int i=1;i<=n+1;i++)
        {
            mx[i]=-1LL*INF*INF;
            ll tpmx=w[sk[top]],tpmi=w[sk[top]];
            while(top&&he[i]<=he[sk[top]])
            {
                R[sk[top]]=i;
                rmx[sk[top]]=tpmx;
                rmi[sk[top]]=tpmi;
                tpmx=max(tpmx,lmx[sk[top]]);
                tpmi=min(tpmi,lmi[sk[top]]);
                top--;
            }
            L[i]=sk[top];
            lmx[i]=tpmx;
            lmi[i]=tpmi;
            sk[++top]=i;
        }
        int num=0;
        for(int i=2;i<=n;i++)
        {
            num=max(num,he[i]);
            mx[he[i]]=max(mx[he[i]],lmx[i]*rmx[i]);
            mx[he[i]]=max(mx[he[i]],lmi[i]*rmi[i]);
            sum[he[i]]+=1LL*(i-L[i])*(R[i]-i);
        }
        for(int i=num+1;i<=n;i++)mx[i]=0;
        for(int i=num-1;i>=0;i--)mx[i]=max(mx[i],mx[i+1]),sum[i]+=sum[i+1];
        for(int i=0;i<=n-1;i++)printf("%lld %lld\n",sum[i],mx[i]);
    }
}A;
int main()
{
#ifndef ONLINE_JUDGE
    freopen("aa.in","r",stdin);
#endif
    read(A.n);
    for(int i=1;i<=A.n;i++)read_char(A.s[i]);
    A.BuildKth();
    A.GetHeight();
    for(int i=1;i<=A.n;i++)read(w[A.rk[i]]);
    A.solve();
}