洛谷 题解 P2119【魔法阵】

很好的一道数学推导题

45分做法

\(O(N^4)\)

暴力枚举四个材料

55分做法

从第一个约束条件可得到所有可行答案都是单调递增的，所以可以排序一遍，减少枚举量，可以拿到55分

100分做法

首先可以发现每个x都小于n，而n最大值只是15000，所以可以开一个桶来存每个魔法值出现的次数

回忆一下3个约束条件

\(xa<xb<xc<xd\)①

\(xb-xa=2(xd-xc)\)②

\(xb-xa<(xc-xb)/3\)③

现在魔改一下这三个式子

设\(t=xd-xc\)

所以②可化为\(xb-xa=2t\)④

将④代入③

\(2t<(xc-xb)/3\)

移项一下，就变成

\(6t<xc-xb\)⑤

再魔改一下

设\(6t+k=xc-xb\)（就是把差的部分补上去）

于是可以画出来一个图

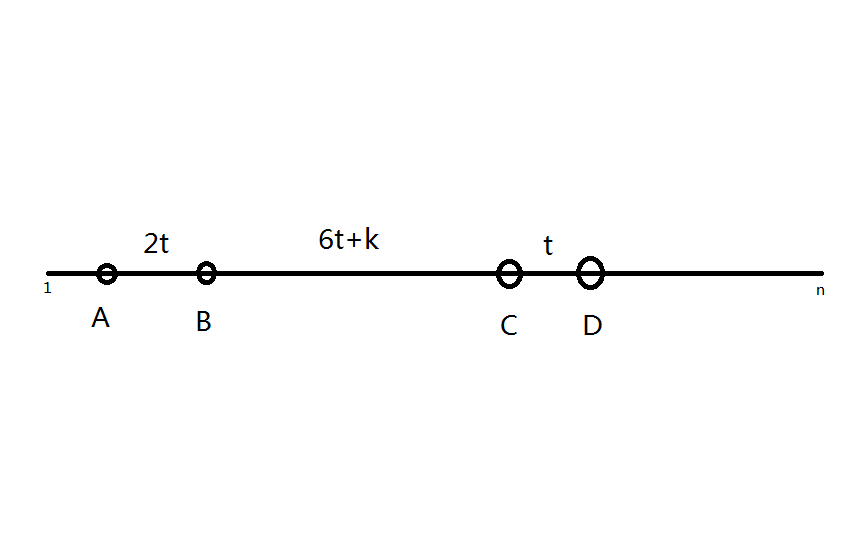
显然，A的最小值为1，D的最大值为n

由图可得\(AD=9t+k\)

所以我们可以尝试着枚举t，用t来表示各个魔法值的值

由上易得t的范围为\(1<=t<=(n-1)/9\)

再枚举D，因为我们已经枚举出了t，所以C的值是可以直接算出来的

\(C=D-t\)

又因为使A,B,C,D满足条件的k的最小值为1，所以对于当前的C和D，最大的A和B为\(A=D-9t-1\),\(B=D-7t-1\)

那么如果A和B更小怎么办？

观察到在其他条件不变的情况下，只要CC和BB满足\(Xc-Xb>6t\)，那么这个魔法阵就一定成立，所以当\((a1<a2,b1<b2)\)时，只要a2和b2能够和C,D组成魔法阵，a1,b1也一定能和C,D组成魔法阵，所以可以使用前缀和优化

然后又由乘法原理可得，当前魔法值作为DD物品的个数为\(SumD=SumA*SumB*SumC\)

所以我们利用前缀和优化\(SumA*SumB\)

C的情况可以顺便在算D的时候算出来

那么还有一个问题是，我们枚举的D的范围是多少？

因为要统计前缀和，所以一定是要顺推下去的，由上面那张图我们可以知道，D的最大值为n，最小值则为当k=1且A=1的时候，所以D的最小值为\(9*t+2\)，再小是无法组成魔法阵的

同理可以枚举A

但是这个的情况又和枚举D的情况有一点不同

在其他条件不变的情况下，只要C和B满足\(Xc−Xb>6t\)，那么这个魔法阵就一定成立，所以当\((c1<c2,d1<d2)\)时，只要c1和d1能够和A,B组成魔法阵，c2,d2也一定能和A,B组成魔法阵，所以可以使用后缀和优化

因为需要统计后缀和，所以需要逆推

枚举的范围：A的最大值为\((n−t∗9−1)\)(因为当k=1，D=n的时候A才最大)，A的最小值则为1

所以就可以算出每个魔法值作为A,B,C,D物品的次数了，输出时直接输出当前魔法物品的魔法值的次数就可以了

代码：

#include<bits/stdc++.h>
using namespace std;
const int MAXN=15000+10;
const int MAXM=40000+10;
int n,m;
int x[MAXM],v[MAXN];
int a[MAXN],b[MAXN],c[MAXN],d[MAXN];
inline int read()
{
	int tot=0;
	char c=getchar();
	while(c<'0'||c>'9')
		c=getchar();
	while(c>='0'&&c<='9')
	{
		tot=tot*10+c-'0';
		c=getchar();
	}
	return tot;
}
int main()
{
	n=read();m=read();
	for(int i=1;i<=m;i++)
	{
		x[i]=read();
		v[x[i]]++;
	}
	for(int t=1;t<=(n-1)/9;t++)
	{
		int sum=0;
		for(int D=9*t+2;D<=n;D++)
		{
			int A=D-9*t-1,B=D-7*t-1,C=D-t;
			sum+=v[A]*v[B];
			c[C]+=v[D]*sum;
			d[D]+=v[C]*sum;
		}
		sum=0;
		for(int A=n-9*t-1;A>=1;A--)
		{
			int B=A+2*t,C=8*t+1+A,D=9*t+1+A;
			sum+=v[C]*v[D];
			a[A]+=v[B]*sum;
			b[B]+=v[A]*sum;
		}
	}
	for(int i=1;i<=m;i++)
	cout<<a[x[i]]<<" "<<b[x[i]]<<" "<<c[x[i]]<<" "<<d[x[i]]<<endl;
	return 0;
}

参考博客