Islands and Bridges（POJ2288+状压dp+Hamilton 回路）

题目链接：http://poj.org/problem?id=2288

题目：

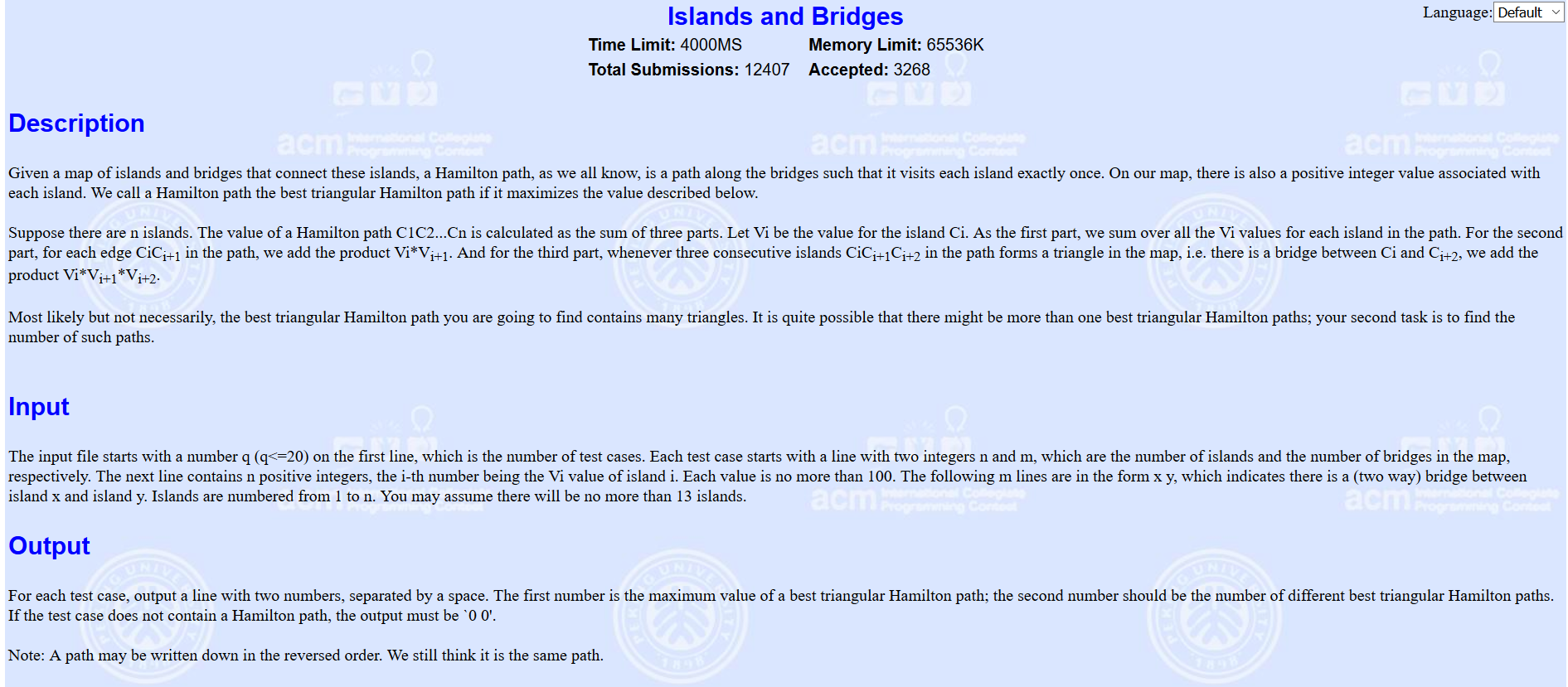
题意：求Hamilton 路径权值的最大值，且求出有多少条权值这么大的Hamilton路径。

思路：状压dp，dp[i][j][k]表示第i种状态下倒数第二个岛屿为j倒数第一个岛屿为k下的权值，cnt[i][j][k]记录条数。

　　当有边(i,j)存在时，有如下初值可赋：
　　d[(1<<i)+(1<<j)][i][j]=val[i]+val[j]+val[i]*val[j],cnt[(1<<i)+(1<<j)][i][j]=1。
　　
如果状态（state,i,j）可达，检查岛k，如果此时k没有被访问过并且有边(j,k)存在，则做如下操作：
　　1）设tmp为下一步访问岛k时获得的总利益，r=state+(1<<k)。
　　2）如果tmp>d[r][j][k]，表示此时可以更新到更优解，则更新：
　　    d[r][j][k]=tmp,cnt[r][j][k]=cnt[state][i][j]。
　　3）如果tmp==d[r][j][k]，表示此时可以获得达到局部最优解的更多方式，则更新：
    　　cnt[r][j][k]+=cnt[state][i][j]。
　　最后检查所有的状态（(1<<n)-1,i,j），叠加可以得到最优解的道路数。
　　需要注意的是，题目约定一条路径的两种行走方式算作一种，所以最终结果要除2。

代码实现如下：

 #include <set>
 #include <map>
 #include <queue>
 #include <stack>
 #include <cmath>
 #include <bitset>
 #include <cstdio>
 #include <string>
 #include <vector>
 #include <cstdlib>
 #include <cstring>
 #include <iostream>
 #include <algorithm>
 using namespace std;

 typedef long long ll;
 typedef pair<ll, ll> pll;
 typedef pair<ll, int> pli;
 typedef pair<int, ll> pil;;
 typedef pair<int, int> pii;
 typedef unsigned long long ull;

 #define lson i<<1
 #define rson i<<1|1
 #define bug printf("*********\n");
 #define FIN freopen("D://code//in.txt", "r", stdin);
 #define debug(x) cout<<"["<<x<<"]" <<endl;
 #define IO ios::sync_with_stdio(false),cin.tie(0);

 const double eps = 1e-;
 const int mod = ;
 const int maxn = (<<) + ;
 const double pi = acos(-);
 const int inf = 0x3f3f3f3f;
 const ll INF = 0x3f3f3f3f3f3f3f;

 int t, n, m, u, v;
 int w[], mp[][];
 ll dp[maxn][][], cnt[maxn][][];

 int main() {
     //FIN;
     scanf("%d", &t);
     while(t--) {
         memset(mp, , sizeof(mp));
         memset(dp, -, sizeof(dp));
         memset(cnt, , sizeof(cnt));
         scanf("%d%d", &n, &m);
         for(int i = ; i <= n; ++i) {
             scanf("%d", &w[i]);
         }
         for(int i = ; i <= m; ++i) {
             scanf("%d%d", &u, &v);
             mp[u][v] = mp[v][u] = ;
         }
         if(n == ) {
             printf("%d 1\n", w[]);
             continue;
         }
         for(int i = ; i <= n; ++i) {
             for(int j = ; j <= n; ++j) {
                 if(i != j && mp[i][j]) {
                     dp[(<<(i-))|(<<(j-))][i][j] = w[i] + w[j] + (ll) w[i] * w[j];
                     cnt[(<<(i-))|(<<(j-))][i][j] = ;
                 }
             }
         }
         int tot =  << n;
         for(int i = ; i < tot; ++i) {
             for(int j = ; j <= n; ++j) {
                 if(i & (<<(j-))) {
                     for(int k = ; k <= n; ++k) {
                         if(j != k && (i & (<<(k-))) && mp[j][k] && dp[i][j][k] != -) {
                             for(int x = ; x <= n; ++x) {
                                 if(j != x && k != x && mp[k][x] && (i & (<<(x-))) == ) {
                                     ll tmp = dp[i][j][k] + w[x] + (ll)w[k] * w[x];
                                     if(mp[j][x]) tmp += (ll)w[k] * w[j] * w[x];
                                     if(tmp > dp[i|(<<(x-))][k][x]) {
                                         dp[i|(<<(x-))][k][x] = tmp;
                                         cnt[i|(<<(x-))][k][x] = cnt[i][j][k];
                                     } else if(tmp == dp[i|(<<(x-))][k][x]){
                                         cnt[i|(<<(x-))][k][x] += cnt[i][j][k];
                                     }
                                 }
                             }
                         }
                     }
                 }
             }
         }
         ll ans1 = , ans2 = ;
         for(int i = ; i <= n; ++i) {
             for(int j = ; j <= n; ++j) {
                 if(i == j) continue;
                 if(dp[tot-][i][j] > ans1) {
                     ans1 = dp[tot-][i][j];
                     ans2 = cnt[tot-][i][j];
                 } else if(dp[tot-][i][j] == ans1) {
                     ans2 += cnt[tot-][i][j];
                 }
             }
         }
         printf("%lld %lld\n", ans1, ans2 / );
     }
     return ;
 }