【剑指offer】圆圈中最后剩下的数字（约瑟夫问题），C++实现

原创博文，转载请注明出处！

# 题目

# 思路

本题即为典型的约瑟夫问题，通过递推公式倒推出问题的解。原始问题是从n个人中每隔m个数踢出一个人，原始问题变成从n-1个人中每隔m个数踢出一个人……

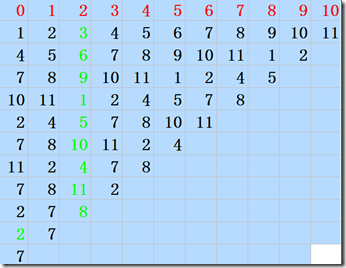
      第一行表示每个人的下标，现在要从11个人中删除报数为3的人，从图中可以可看出最后7是胜利者。分析其中的规律：

第一轮中，11个人中胜利者7的角标是6；

第二轮中，10个人中胜利者7的角标是3；

第三轮中，9个人中胜利者7的角标是0；

第四轮中，8个人中胜利者7的角标是6；

第五轮中，7个人中胜利者7的角标是3；

第六轮中，6个人中胜利者7的角标是0；

第七轮中，5个人中胜利者7的角标是3；

第八轮中，4个人中胜利者7的角标是0；

第九轮中，3个人中胜利者7的角标是1；

第十轮中，2个人中胜利者7的角标是1；

第十一轮中，1个人中胜利者7的角标是0；

从第十一轮中倒推到第一轮：

从第十一轮中推出第十轮的角标数，f(2,3) = (f(1,3) + m) % 2 =(0+3) % 2 = 1

从第十轮中推出第九轮的角标数，f(3,3) = (f(2,3) + m) % 3 =(1+3) % 3 = 1

从第九轮中推出第八轮的角标数，f(4,3) = (f(3,3) + m) % 4 =(1+3) % 4 = 0

懒得写了…….

结论：从n个人中每隔m删除一人，递推公式为 f(n,m) = (f(n-1,m)+m)  %  n

# 代码

#include <iostream>
using namespace std;

class Solution {
public:
    // n表示多少个人，m表示随机数
    int LastRemaining_Solution(int n, int m)
    {
        // 特殊输入
        if(n == 0 || m < 0) return -1;

        // 递推公式计算
        int res = 0;
        for(int i = 1; i <= n; i++)
        {
            res = (res + m) % i;
            cout<<res<<endl;
        }
        return res;
    }
};
int main()
{
    int n = 11;
    int m = 3;
    Solution solution;
    solution.LastRemaining_Solution(n,m);
    return 0;
}