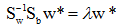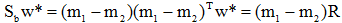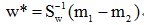【线性判别】Fisher线性判别(转)
今天读paper遇到了Fisher线性判别的变体, 所以来学习一下, 所以到时候一定要把PRMl刷一遍呀
以下两篇论文一起阅读比较好:
论文1: https://blog.csdn.net/Rainbow0210/article/details/52892805
在前文《贝叶斯决策理论》中已经提到,很多情况下,准确地估计概率密度模型并非易事,在特征空间维数较高和样本数量较少的情况下尤为如此。
实际上,模式识别的目的是在特征空间中设法找到两类(或多类)的分类面,估计概率密度函数并不是我们的目的。
前文已经提到,正态分布情况下,贝叶斯决策的最优分类面是线性的或者是二次函数形式的,本文则着重讨论线性情况下的一类判别准则——Fisher判别准则。
为了避免陷入复杂的概率的计算,我们直接估计判别函数式中的参数(因为我们已经知道判别函数式是线性的)。
首先我们来回顾一下线性判别函数的基本概念:




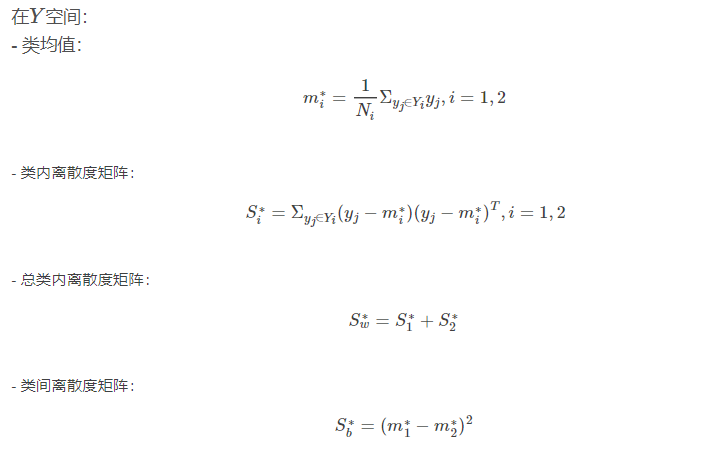


第二篇: https://blog.csdn.net/qq_18870127/article/details/79097735
应用统计方法解决模式识别问题时,一再碰到的问题之一就是维数问题。在低维空间里解析上或计算上行得通的方法,在高维空间里往往行不通。因此,降低维数有时就会成为处理实际问题的关键。
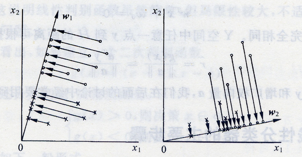
问题描述:如何根据实际情况找到一条最好的、最易于分类的投影线,这就是Fisher判别方法所要解决的基本问题。
考虑把d维空间的样本投影到一条直线上,形成一维空间,即把维数压缩到一维。然而,即使样本在d维空间里形成若干紧凑的互相分得开的集群,当把它们投影到一条直线上时,也可能会是几类样本混在一起而变得无法识别。但是,在一般情况下,总可以找到某个方向,使在这个方向的直线上,样本的投影能分得开。下图可能会更加直观一点:
从d维空间到一维空间的一般数学变换方法:假设有一集合Г包含N个d维样本x1, x2, …, xN,其中N1个属于ω1类的样本记为子集Г1, N2个属于ω2类的样本记为子集Г2 。若对xn的分量做线性组合可得标量:
yn = wTxn, n=1,2,…,N
这样便得到N个一维样本yn组成的集合,并可分为两个子集Г1’和Г2’ 。
实际上,w的值是无关紧要的,它仅是yn乘上一个比例因子,重要的是选择w的方向。w的方向不同,将使样本投影后的可分离程度不同,从而直接影响的分类效果。因此,上述寻找最佳投影方向的问题,在数学上就是寻找最好的变换向量w*的问题。
Fisher准则函数的定义
几个必要的基本参量:
1.
在d维X空间
(1)各类样本的均值向量mi
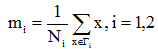
(2)样本类内离散度矩阵Si和总样本类内离散度矩阵Sw
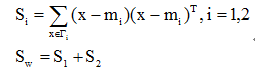
其中Sw是对称半正定矩阵,而且当N>d时通常是非奇异的。(半正定矩阵:特征值都不小于零的实对称矩阵;非奇异矩阵:矩阵的行列式不为零)
(3)样本类间离散度矩阵Sb
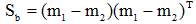
Sb是对称半正定矩阵。
2. 在一维Y空间
(1)各类样本的均值
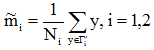
(2)样本类内离散度 和总样本类内离散度
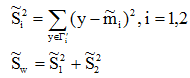
我们希望投影后,在一维Y空间中各类样本尽可能分得开些,即希望两类均值之差越大越好,同时希望各类样本内部尽量密集,即希望类内离散度越小越好。
Fisher准则函数定义
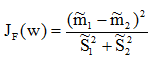
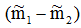 是两类均值之差,
是两类均值之差,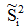 是样本类内离散度。显然,应该使JF(w)的分子尽可能大而分母尽可能小,即应寻找使JF(w)尽可能大的w作为投影方向。但上式中并不显含w,因此须设法将JF(w)变成w的显函数。
是样本类内离散度。显然,应该使JF(w)的分子尽可能大而分母尽可能小,即应寻找使JF(w)尽可能大的w作为投影方向。但上式中并不显含w,因此须设法将JF(w)变成w的显函数。由各类样本的均值可推出:
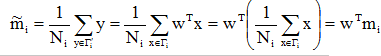
这样,Fisher准则函数JF(w)的分子可写成:
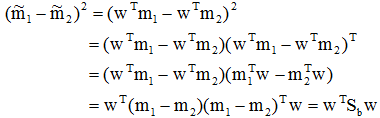
现在再来考察JF(w)的分母与w的关系:
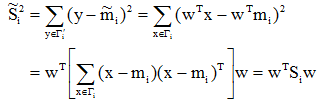
因此,
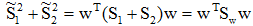
将上述各式代入JF(w),可得:
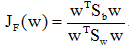
其中Sb为样本类间离散度矩阵,Sw为总样本类内离散度矩阵。
最佳变换向量w的求取
为求使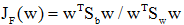
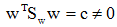
定义Lagrange函数为:
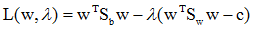
其中λ为Lagrange乘子。将上式对w求偏导数,可得:
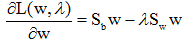
令偏导数为零,有;
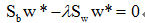
即
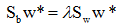
其中w就是JF(w)的极值解。因为Sw非奇异,将上式两边左乘 上式为求一般矩阵 其中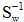
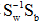
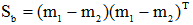
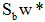
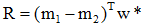
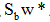
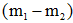
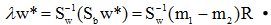
从而可得:
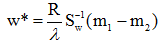
由于我们的目的是寻找最佳的投影方向,w的比例因子对此并无影响,因此可忽略比例因子R/λ,有: w
【线性判别】Fisher线性判别(转)的更多相关文章
- 线性判别函数-Fisher 线性判别
这是我在上模式识别课程时的内容,也有参考这里. 线性判别函数的基本概念 判别函数为线性的情况的一般表达式 式中x是d 维特征向量,又称样本向量, 称为权向量, 分别表示为 是个常数,称为阈值权. 设样 ...
- PRML读书会第四章 Linear Models for Classification(贝叶斯marginalization、Fisher线性判别、感知机、概率生成和判别模型、逻辑回归)
主讲人 planktonli planktonli(1027753147) 19:52:28 现在我们就开始讲第四章,第四章的内容是关于 线性分类模型,主要内容有四点:1) Fisher准则的分类,以 ...
- Fisher线性判别分析
Fisher线性判别分析 1.概述 在使用统计方法处理模式识别问题时,往往是在低维空间展开研究,然而实际中数据往往是高维的,基于统计的方法往往很难求解,因此降维成了解决问题的突破口. 假设数据存在于d ...
- PS图层混合算法之二(线性加深,线性减淡,变亮,变暗)
线性加深模式: 查看每个通道的颜色信息,通过降低"亮度"使底色的颜色变暗来反映绘图色,和白色混合没变化. Linear Burn 线形加深 C=A+B-1 如果上下层的像素值之和小 ...
- 机器学习理论基础学习3.2--- Linear classification 线性分类之线性判别分析(LDA)
在学习LDA之前,有必要将其自然语言处理领域的LDA区别开来,在自然语言处理领域, LDA是隐含狄利克雷分布(Latent Dirichlet Allocation,简称LDA),是一种处理文档的主题 ...
- fisher线性判别
fisher 判决方式是监督学习,在新样本加入之前,已经有了原样本. 原样本是训练集,训练的目的是要分类,也就是要找到分类线.一刀砍成两半! 当样本集确定的时候,分类的关键就在于如何砍下这一刀! 若以 ...
- Fisher 线性判别
Multiplying both sides of this result by wT and adding w0, and making use of y(x)=wTx+w0 and y(xΓ)= ...
- 数据结构C语言实现系列——线性表(线性表链接存储(单链表))
#include <stdio.h>#include <stdlib.h>#define NN 12#define MM 20typedef int elemType ;/** ...
- 线性表&顺序线性表
第二章 线性表 参考文献:[数据结构(C语言版)].严蔚敏 本篇章仅为个人学习数据结构的笔记,不做任何用途. 2.1 线性结构的特点 (1). 存在唯一的一个被称为"第一个"的数据 ...
随机推荐
- 自定义HTTP头时的注意事项(转)
原文:https://blog.gnuers.org/?p=462 HTTP头是可以包含英文字母([A-Za-z]).数字([0-9]).连接号(-)hyphens, 也可义是下划线(_).在使用ng ...
- Cache与主存之间的全相联映射,直接映射和组相联映射的区别
2017-02-22 注:本文并非原创,来自百度文库,只是觉得写得较好,故分享之.若是某人的知识产权,望告知!谢谢 1.高速缓冲存储器的功能.结构与工作原理 高速缓冲存储器是存在于主存与CPU之间的一 ...
- Python垃圾回收机制详解转自--Kevin Lu
一.垃圾回收机制 Python中的垃圾回收是以引用计数为主,分代收集为辅.引用计数的缺陷是循环引用的问题. 在Python中,如果一个对象的引用数为0,Python虚拟机就会回收这个对象的内存. #e ...
- Elasticsearch.js 发布 —— 在Node.js和浏览器中调用Elasticsearch
继PHP.Ruby.Python和Perl之后,Elasticsearch最近发布了Elasticsearch.js,Elasticsearch的JavaScript客户端库.可以在Node.js和浏 ...
- go-008-循环语句
一.循环语句[只有for] 1.基础结构: Go语言的For循环有3中形式,只有其中的一种使用分号. 和 C 语言的 for 一样: for init; condition; post { } 和 C ...
- 17.出现fatal signal(SIGSEGV),code 1,fault addr 0x0 in tid 29931的问题
原因是: 在onCreate方法里面调一些东西的时候,有时候系统相关的东西还没有初始化完,你的代码就已经执行了,会出现一些问题 解决方法: 增加延时1s /一.第一步初始化,此处用的是demo的ap ...
- 创建Java不可变型的枚举类型Gender
创建Java不可变型的枚举类型,其实例如下: // 创建不可变型的枚举类 enum Gender { // 此处的枚举值必须调用对应的构造器来创建 MALE("男"), FEMAL ...
- 控制台应用程序中添加对MFC的支持
在windows控制台应用程序中,肯能会想使用一些MFC中的类,如CStringArray等,通过下面两步简单的设置可以添加对MFC的支持: 1.右击工程名 -> References 选择 A ...
- delphi 正则表达式
常用正则表式 正则表达式用于字符串处理.表单验证等场合,实用高效.现将一些常用的表达式收集于此,以备不时之需. 匹配中文字符的正则表达式: [\u4e00-\u9fa5] 评注:匹配中文还真是个头疼的 ...
- php写守护进程(转载 http://blog.csdn.net/tengzhaorong/article/details/9764655)
守护进程(Daemon)是运行在后台的一种特殊进程.它独立于控制终端并且周期性地执行某种任务或等待处理某些发生的事件.守护进程是一种很有用的进程.php也可以实现守护进程的功能. 1.基本概念 进程 ...