Codeforces Round #360 (Div. 2) D. Remainders Game

D. Remainders Game

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Today Pari and Arya are playing a game called Remainders.

Pari chooses two positive integer x and k, and tells Arya k but not x. Arya have to find the value 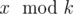. There are n ancient numbers c1, c2, ..., cn and Pari has to tell Arya  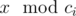if Arya wants. Given k and the ancient values, tell us if Arya has a winning strategy independent of value of x or not. Formally, is it true that Arya can understand the value  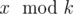for any positive integer x?

Note, that 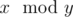 means the remainder of x after dividing it by y.

Input

The first line of the input contains two integers n and k (1 ≤ n,  k ≤ 1 000 000) — the number of ancient integers and value k that is chosen by Pari.

The second line contains n integers c1, c2, ..., cn (1 ≤ ci ≤ 1 000 000).

Output

Print "Yes" (without quotes) if Arya has a winning strategy independent of value of x, or "No" (without quotes) otherwise.

Examples

input

4 5
2 3 5 12

output

Yes

input

2 7
2 3

output

No

Note

In the first sample, Arya can understand 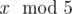 because 5 is one of the ancient numbers.

In the second sample, Arya can't be sure what 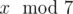 is. For example 1 and 7 have the same remainders after dividing by 2 and 3, but they differ in remainders after dividing by 7.

题意：给你n个数，一个k；可以告诉你xmod ci的值；求x%k是否唯一；

思路：根据中国剩余定理，如果中国剩余定理有解x，另外一个解为x+lcm(c0,c1...cn);

　　　 所以lcm%k==0；

#include<bits/stdc++.h>
using namespace std;
#define ll __int64
#define mod 1000000007
#define pi (4*atan(1.0))
const int N=1e3+,M=1e6+,inf=1e9+;
ll gcd(ll a,ll b)
{
    return b==?a:gcd(b,a%b);
}
int main()
{
    ll x,y,z,i,t;
    ll lcm=;
    scanf("%lld%lld",&x,&y);
    for(i=;i<x;i++)
    {
        scanf("%lld",&z);
        lcm=z*lcm/gcd(z,lcm);
        lcm%=y;
    }
    if(lcm==)
    printf("Yes\n");
    else
    printf("No\n");
    return ;
}