BZOJ4502串——AC自动机(fail树)

题目描述

兔子们在玩字符串的游戏。首先，它们拿出了一个字符串集合S，然后它们定义一个字

符串为“好”的，当且仅当它可以被分成非空的两段，其中每一段都是字符串集合S中某个字符串的前缀。

比如对于字符串集合{"abc","bca"}，字符串"abb"，"abab"是“好”的（"abb"="ab"+"b",abab="ab"+"ab"），而字符串“bc”不是“好”的。

兔子们想知道，一共有多少不同的“好”的字符串。

输入

第一行一个整数n，表示字符串集合中字符串的个数

接下来每行一个字符串

输出

一个整数，表示有多少不同的“好”的字符串

样例输入

2
ab
ac

样例输出

9

提示

1<=n<=10000，每个字符串非空且长度不超过30，均为小写字母组成。

因为trie树上每个点到根都是一个前缀，所以假设trie树上有cnt个点，最多就能有cnt^2个“好”字符串，但有些情况是重复的，比如：字符串集合里有aa和ab连个串，那么‘aa’+‘b'和‘a’+‘ab’在本质上是一个串。所以只要把重复的都去掉就是问题的答案了。如下图所示，

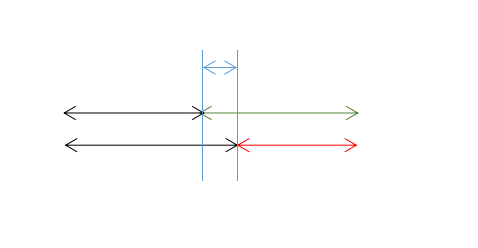
绿串和短黑串与红串和长黑串就属于重复的答案，我们取红串和长黑串为记录的答案，就要把绿串的这种情况去掉。可以发现在AC自动机上，红串是绿串的后缀，蓝串是长黑串的后缀，所以对于每个红串与绿串，它们相差的部分(也就是蓝串)是几个串的后缀(就相当于有几个能和红串、绿串匹配的黑串)，就要把答案相应的减去多少。在fail树上就转化成了以蓝串的末端点为根的子树中有多少个节点（不算本身，因为本身代表自己是自己的后缀，那么绿串前面的黑串就是空串）。所以对于AC自动机上每个fail指针不为根节点的节点(如果fail指针是根节点它就没有后缀)，找它和它fail指针指向的串相差的部分所组成的串，用总答案减掉在fail树上子树大小就是最终结果。

#include<cmath>
#include<queue>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
int n;
int cnt;
int num;
char s[40];
long long ans;
int f[300010];
int fail[300010];
int a[300010][26];
long long sum[300010];
void build(char *s)
{
    int now=0;
    int len=strlen(s);
    for(int i=0;i<len;i++)
    {
        if(!a[now][s[i]-'a'])
        {
            a[now][s[i]-'a']=++cnt;
            f[cnt]=now;
        }
        now=a[now][s[i]-'a'];
    }
}
void getfail()
{
    queue<int>q;
    for(int i=0;i<26;i++)
    {
        if(a[0][i])
        {
            fail[a[0][i]]=0;
            q.push(a[0][i]);
        }
    }
    while(!q.empty())
    {
        int now=q.front();
        q.pop();
        for(int i=0;i<26;i++)
        {
            if(a[now][i])
            {
                fail[a[now][i]]=a[fail[now]][i];
                q.push(a[now][i]);
            }
            else
            {
                a[now][i]=a[fail[now]][i];
            }
        }
    }
    return ;
}
void solve()
{
    for(int i=1;i<=cnt;i++)
    {
        for(int j=fail[i];j;j=fail[j])
        {
            sum[j]++;
        }
    }
    for(int i=1;i<=cnt;i++)
    {
        if(fail[i])
        {
            int j=i;
            int k=fail[i];
            while(k)
            {
                j=f[j];
                k=f[k];
            }
            ans-=sum[j];
        }
    }
}
int main()
{
    scanf("%d",&n);
    for(int i=0;i<n;i++)
    {
        scanf("%s",s);
        build(s);
    }
    getfail();
    ans=1ll*cnt*cnt;
    solve();
    printf("%lld",ans);
    return 0;
}