【立体几何】Journey to Jupiter Gym - 101991J 立体几何模板

https://cn.vjudge.net/problem/Gym-101991J

题目很长，其实就是给你一个正三角形，并且告诉你它的中点在Z轴上以及法向量，边长和顶点A的坐标（自由度已定），让你求A，B，C到Z轴上一点H的距离。

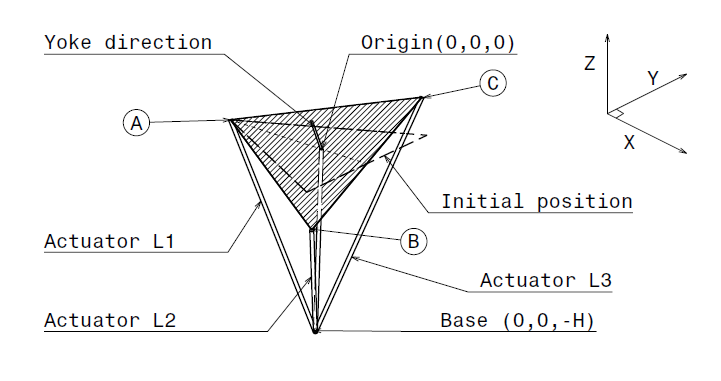
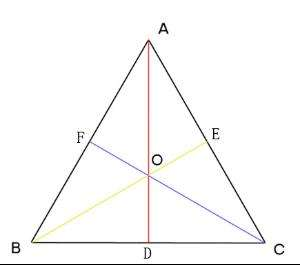
题解：高考向量题，考虑正三角形ABC，我们把OB拆成OD加DB，OD=-OA/2，DB可以通过连立三个方程得到（它垂直于AO和法向量，他的长度为L/2)

坑：

我一开始拆的是OA+AB，公式太长不可解orz，

后来解方程的时候写错了orz

然后y写成xorz

最后没考虑逆时针输出orz（这里要用叉积判一下，OA X OB 的方向要与法向量同）

#include<algorithm>
#include<iostream>
#include<stdlib.h>
#include<string.h>
#include<math.h>
#include<stdio.h>
#include<vector>
#include<queue>
#include<string>
#include<ctime>
#include<stack>
#include<map>
#include<set>
#include<list>
using namespace std;
#define rep(i,j,k) for(int i = (int)j;i <= (int)k;i ++)
#define per(i,j,k) for(int i = (int)j;i >= (int)k;i --)
#define debug(x) cerr<<#x<<" = "<<(x)<<endl
#define mmm(a,b) memset(a,b,sizeof(a))
#define pb push_back
//#define x first
//#define y second

typedef double  db;
typedef long long ll;
const int MAXN = ;;
const int maxn = MAXN;
struct V {
    db x, y,z;
    V() {}
    void sc() { scanf("%lf%lf", &x, &y); }
    V(db a, db b) : x(a), y(b) { }
    V operator+(V o) { return V(x + o.x, y + o.y); }
    V operator-(V o) { return V(x - o.x, y - o.y); }
    db L() { return sqrt(x * x + y * y); }
    V N() {
        db l = L();
        return V(x / l, y / l);
    }
    V rot(db th) { return V(x * cos(th) - y * sin(th), x * sin(th) + y * cos(th)); }
    V operator*(db z) { return V(x * z, y * z); }
    db operator*(V o) { return x * o.x + y * o.y; }
    db operator|(V o) { return x * o.y - o.x * y; }
    void pr() { printf("%lf %lf\n", x, y); }
} p[maxn];

//三维几何函数库

#define eps 1e-8
#define zero(x) (((x)>0?(x):-(x))<eps)
struct point3 { db x, y, z; };
struct line3 { point3 a, b; };
struct plane3 { point3 a, b, c; };

//计算cross product U x V
point3 xmult(point3 u, point3 v) {
    point3 ret;
    ret.x = u.y*v.z - v.y*u.z;
    ret.y = u.z*v.x - u.x*v.z;
    ret.z = u.x*v.y - u.y*v.x;
    return ret;
}

//计算dot product U . V
db dmult(point3 u, point3 v) {
    return u.x*v.x + u.y*v.y + u.z*v.z;
}

//矢量差 U - V
point3 subt(point3 u, point3 v) {
    point3 ret;
    ret.x = u.x - v.x;
    ret.y = u.y - v.y;
    ret.z = u.z - v.z;
    return ret;
}
point3 addt(point3 u, point3 v) {
    point3 ret;
    ret.x = u.x + v.x;
    ret.y = u.y + v.y;
    ret.z = u.z + v.z;
    return ret;
}

//取平面法向量
point3 pvec(plane3 s) {
    return xmult(subt(s.a, s.b), subt(s.b, s.c));
}
point3 pvec(point3 s1, point3 s2, point3 s3) {
    return xmult(subt(s1, s2), subt(s2, s3));
}

//两点距离,单参数取向量大小
db distance(point3 p1, point3 p2) {
    return sqrt((p1.x - p2.x)*(p1.x - p2.x) + (p1.y - p2.y)*(p1.y - p2.y) + (p1.z - p2.z)*(p1.z - p2.z));
}

//向量大小
db vlen(point3 p) {
    return sqrt(p.x*p.x + p.y*p.y + p.z*p.z);
}

int main() {
    freopen("jupiter.in", "r", stdin);
    int t; cin >> t;
    while (t--) {
        point3 N, A;
        db l, h;
        scanf("%lf%lf%lf%lf%lf%lf%lf%lf", &N.x, &N.y, &N.z, &A.x, &A.y, &A.z, &l, &h);
        //scanf("%f%f%f%f%f%f%f%f", &N.x, &N.y, &N.z, &A.x, &A.y, &A.z, &l, &h);
        //cin >> N.x >> N.y >> N.z >> A.x >> A.y >> A.z >> l >> h;
        point3 H = { .,.,-h };
        db La, Lb, Lc;

        db up = N.z*A.x - A.z*N.x;
        db under = N.y*A.x - A.y*N.x;
        db coy = -up / under;
        db cox =( N.z + N.y*coy)/(-N.x);
        cox = (A.z + A.y*coy) / (-A.x);
        db zz=l*l / 4.0/(coy*coy + cox*cox + 1.0) ;
        db z = l/sqrt(coy*coy + cox * cox + 1.0)/2.0;
        //db z = l / 2.0 / (coy + cox + 1.0);
        db x = cox * z;
        db y = coy * z;
        point3 b = { x,y,z };
        point3 c = { -x,-y,-z };
        point3 t = xmult(A, b);
        if (t.z*N.z > );
        else swap(b, c);
        point3 unA = { -A.x / .,-A.y / .,-A.z / . };
        point3 B = addt(unA, b);
        point3 C = addt(unA, c);
        La = distance(A, H);
        Lb = distance(B, H);
        Lc = distance(C, H);
        //if (N.z < 0)swap(Lb, Lc);
        printf("%.6lf %.6lf %.6lf\n", La,Lb,Lc);

    }
    //cin >> t;
}
/*
2
13 -18 1 7 5 -1 15 12
-12 -17 1 7 -5 -1 15 3

2
13 -18 1 7 5 -1 15 12
-12 -17 1 7 -5 -1 15 3
*/

ps：第一次霸榜？？

然后抄一个三维模板，

这个板子的话就厉害了 ，有了二维向量的一切操作。

这里的旋转操作，可以让向量V绕一个法向量n逆时针转theta度。

于是我们就只有两行代码了，

V3 B = N.rot(A, PI*2.0 / 3.0);
V3 C = N.rot(A, PI*4.0 / 3.0);

#include<algorithm>
#include<iostream>
#include<stdlib.h>
#include<string.h>
#include<math.h>
#include<stdio.h>
#include<vector>
#include<queue>
#include<string>
#include<ctime>
#include<stack>
#include<map>
#include<set>
#include<list>
using namespace std;
#define rep(i,j,k) for(int i = (int)j;i <= (int)k;i ++)
#define per(i,j,k) for(int i = (int)j;i >= (int)k;i --)
#define debug(x) cerr<<#x<<" = "<<(x)<<endl
#define mmm(a,b) memset(a,b,sizeof(a))
#define pb push_back
//#define x first
//#define y second

typedef double  db;
typedef long long ll;
const int MAXN = ;;
const int maxn = MAXN;
const double eps = 1e-;
const double PI = acos(-1.0);
struct V3 {
    db x, y, z;
    V3() {}
    V3(db xx, db yy, db zz) :x(xx), y(yy), z(zz) {}
    void sc() {scanf("%lf%lf%lf", &x, &y, &z);}
    db L() { return sqrt(x*x + y * y + z * z); }
    V3 N() { db l = L(); return V3(x / l, y / l, z / l); }
    V3 operator+(V3 o) { return V3(x + o.x, y + o.y,z+o.z); }
    V3 operator-(V3 o) { return V3(x - o.x, y - o.y,z-o.z); }
    V3 operator*(db zz) { return V3(x * zz, y * zz,z*zz); }
    db operator*(V3 o) { return x * o.x + y * o.y+z*o.z; }
    V3 operator|(V3 o) { return V3(y*o.z-z*o.y,z*o.x-x*o.z,x * o.y - o.x * y); }
};
int sgn(db x) {
    if (fabs(x) < eps)return ;
    else if (x > )return ;
    else return -;
}
struct L3 {
    V3 s, e;
    L3() {}
    L3(V3 ss, V3 ee) :s(ss), e(ee) {}
    V3 rot(V3 p, db arg) {
        if (sgn(((s - p) | (e - p)).L()) == )return p;
        V3 f1 = (e - s) | (p - s);
        V3 f2 = (e - s) | (f1);
        db len = ((s - p) | (e - p)).L() / (s - e).L();
        f1 = f1.N()*len; f2 = f2.N() * len;
        V3 h = p + f2;
        V3 pp = h + f1;
        return h + ((p - h)*cos(arg)) + ((pp - h)*sin(arg));
    }

};

int main() {
    freopen("jupiter.in", "r", stdin);
    int t; cin >> t;
    while (t--) {
        V3 n, A;
        n.sc(); A.sc();
        db L, H;
        scanf("%lf%lf", &L, &H);
        L3 N = L3(V3(, , ), n);
        V3 base = V3(, , -H);
        V3 B = N.rot(A, PI*2.0 / 3.0);
        V3 C = N.rot(A, PI*4.0 / 3.0);
        printf("%.6lf %.6lf %.6lf\n", (base - A).L(), (base - B).L(), (base - C).L());
    }
    //cin >>t;
}
/*
2
13 -18 1 7 5 -1 15 12
-12 -17 1 7 -5 -1 15 3

2
13 -18 1 7 5 -1 15 12
-12 -17 1 7 -5 -1 15 3
*/