Coursera课程《Machine Learning》学习笔记（week2）

1 特征

1-1 什么是特征？

我的理解就是，用于描述某个样本点，以哪几个指标来评定，这些个指标就是特征。比方说对于一只鸟，我们评定的指标就可以是：（a）鸟的翅膀大还是小？（b）鸟喙长还是短？（c）鸟下的蛋是多还是少？等等，这些都能被称之为“鸟”这个样本点的特征。

特征值的数量用“n”来表示。比如我们用一些特征来描述一栋房子，这些特征包括：（a）多少平米？（b）几室几厅？（c）有几层？（d）房子是新还是旧？那么这里就有4个特征，也就是n=4。

1-2 现在我们区分一下符号

（1）m：样本点的数目。

（2）n：特征值的数目。

（3）上标(i)：代表了当前样本点是“第几个样本点”，${x}^{(i)}$是一个向量，里面的每一个元素都是用于描述同一个样本点的不同特征。以下图为例，${x}^{(2)}$就是第二个样本点，它是一个四维列向量，这四个元素分别代表：（a）多少平米？（b）几室几厅？（c）有几层？（d）房子是新还是旧？每一个元素都是一个不同的特征。

（4）下标j：指明了“这是该样本点中哪一个特征”。仍以上图为例，有${x_{2}}^{(3)}$，它是第二个样本点的第三个特征，也就是这栋屋子有2层（numbers of floors）。

（2016.6.30记）

2 梯度下降法技巧

2-1 特征缩放(feature scaling)

2-1-1 狭长的椭圆

当两个特征范围差别比较大时，比方说仍用上面房价那个例子，对于某一个样本点，其房子的大小$x_{1}^{(i)}$范围为0~2000，而卧室数目$x_{2}^{(i)}$的范围为1~5，如果我们只用这两个特征来描述这栋房子，那么其hypothesis有：

$h_{\theta }(x)=\theta_{0}+\theta_{1}x_{1}+\theta_{2}x_{2}$      (2-1)

其cost函数为：

$J(\theta )=\frac{1}{2m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})^{2}$      (2-2)

简单起见，我们假定只有一个样本点，并且忽略掉$\theta _{0}$和label$y$（理解成恰好$\theta _{0}=y$于是刚好一减就没了也未尝不可，总之是为了简化情况），那么这种情况下的cost函数为：

$J(\theta )=\frac{1}{2}(\theta _1x_{1}+\theta _2x_{2})^{2}$      (2-3)

之前我们说过$x_{1}^{(i)}$范围为0~2000，而卧室数目$x_{2}^{(i)}$的范围为1~5，那么不妨令$x_{1}$=2000，$x_{2}$=5。代入式(2-3)，得到cost函数：

$J(\theta )=\frac{1}{2}(2000\theta _1+5\theta _2)^{2}$      (2-4)

把这个式子(2-4)用Python画出来：

import numpy as np
import matplotlib.pyplot as plt
import mpl_toolkits.mplot3d

theta1,theta2=np.mgrid[-500:500:20j,-500:500:20j]
J_theta=0.5*(2000*theta1+5*theta2)**2

ax=plt.subplot(111,projection='3d')
ax.plot_surface(theta1,theta2,J_theta,rstride=1,cstride=1, cmap=plt.cm.hot)
ax.contourf(theta1,theta2,J_theta, zdir='z', offset=-2, cmap=plt.cm.hot)
ax.set_xlabel('theta1')
ax.set_ylabel('theta2')
ax.set_zlabel('J_theta')
plt.show()

得到这样一幅图，其中theta1-theta2平面上的是“theta1-theta2-J_theta”的轮廓图。

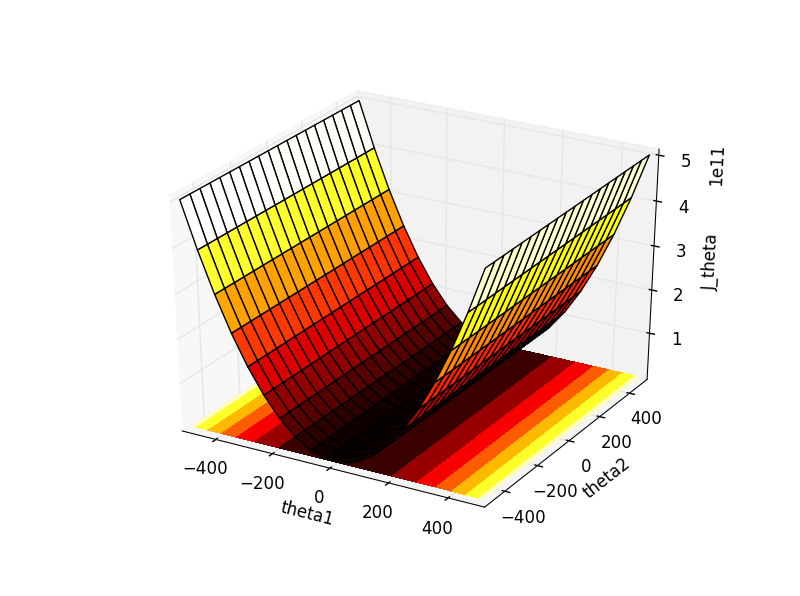
对比一下Ng课件里的这幅轮廓图，我们发现情况是完全吻合的，也就是椭圆沿theta2方向被拉得非常非常长，因此在上面的图中无法一窥椭圆的全貌，各椭圆的侧边近乎是平行的。

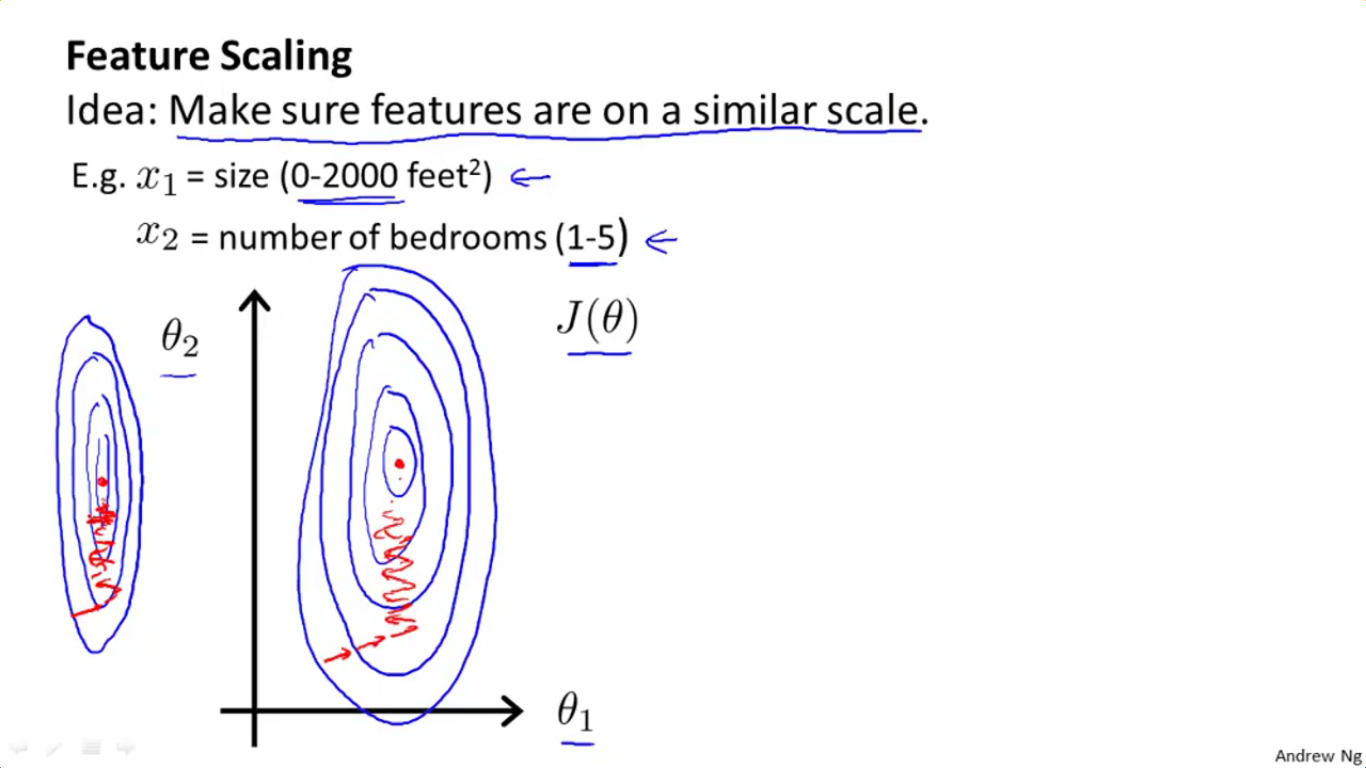
上面我们通过Python绘图演示了椭圆确实被拉得很长这一现象。为了进一步理解为什么会沿theta2方向被拉长，我们再绘制一下$J(\theta )=\theta _1^{2}$的图：

import numpy as np
import matplotlib.pyplot as plt
import mpl_toolkits.mplot3d

theta1,theta2=np.mgrid[-500:500:20j,-500:500:20j]
J_theta=theta1**2

ax=plt.subplot(111,projection='3d')
ax.plot_surface(theta1,theta2,J_theta,rstride=1,cstride=1)
ax.set_xlabel('theta1')
ax.set_ylabel('theta2')
ax.set_zlabel('J_theta')
plt.show()

效果如下：

可以发现$J(\theta )=\frac{1}{2}(2000\theta _1+5\theta _2)^{2}$和$J(\theta )=\theta _1^{2}$的图非常相似。

这说明什么呢？在$\theta _1$强大的权值$2000^2$下，后面那一项$25\theta _2^{2}$几乎可以忽略不计了。更确切地说，同样作为可以影响cost函数$J(\theta )$的变量，$\theta _1$拥有着巨大的权值，使得它只须改变一点点，就会引起cost函数的风云巨变；反之，$\theta _2$只拥有一个很小很小的权值25，这使得$\theta _2$再怎样努力变化，也很难使得cost函数受到影响，所谓人微言轻。这也是为什么在第一幅Python示意图中，$25\theta _2^{2}$几乎没有存在感。

我想我应该把这一部分讲得比较清楚了。

2-1-2 特征缩放

（1）什么是特征缩放

正如2-1-1所述，如果直接把特征1的范围0~2000、特征2的范围1~5拿来用，则会出现一条非常非常狭长的椭圆，这一点将对梯度下降法造成困难，使得梯度下降法的路径非常之复杂（四处乱走，正如上面第二幅图那张课件中红线画的那样）。

解决方案很简单，只需要令：

$x_{1}^{(i)}=\frac{size(feet)}{2000}$
$x_{2}^{(i)}=\frac{(number\ of\ bedrooms)}{5}$

即可将$x_{1}^{(i)}$、$x_{2}^{(i)}$皆规整到一个差不多的范围，这样一来梯度下降法就好进行多了。这种方法被称之为“特征缩放”。

（2）特征缩放的目的

目的：让梯度下降法进行得更快。

2-1-3 均值归一化（Mean Normalization）

这个见最下面那个公式就可以了。使用$\frac{x_1-\mu _1}{S_1}$来替换一个待缩放特征$x_1$，其中：

（1）$S_1$为特征的范围（range=max-min），或者标准偏差。目测这里标准偏差才是各种paper和book通用的，不过为了降低难度，Ng说直接使用$S_1=max-min$就可以；

（2）$\mu _1$则是训练样本点$x_1$的平均值，这跟概率论中的表述是一样的。就拿$x_1$的范围为0~2000为例，那么它的平均值$\mu _1$=(0+2000)/1000；而$x_2$的范围为1~5为例，那么它的平均值$\mu _2$=(1+5)/2=3。

（2016.7.4记）

（未完待续）

by 悠望南山