（六）6.7 Neurons Networks whitening

PCA的过程结束后，还有一个与之相关的预处理步骤，白化（whitening）

对于输入数据之间有很强的相关性，所以用于训练数据是有很大冗余的，白化的作用就是降低输入数据的冗余，通过白化可以达到（1）降低特征之间的相关性（2）所有特征同方差，白化是需要与平滑与PCA结合的，下边来看如何结合。

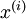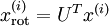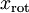对于训练数据{}，找到其所有特征组成的新基U，计算在新基的坐标 ，这里就会消除数据的相关性：

这个数据的协方差矩阵如下：

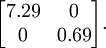
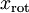 协方差矩阵对角元素的值为  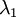和 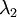 ，且非对角线元素取值为0，课件不同纬度的特征之间是不相关的，对应的  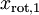和 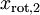 是不相关的，这便满足白化的第一个要求，降低相关性，下面就要使特征之间同方差（注意是变化后的特征同方差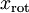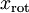）中每个特征 i 的方差为  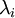我们可以直接使用  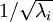作为缩放因子来缩放每个特征  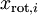。具体地，我们定义白化后的数据  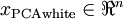如下：

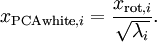
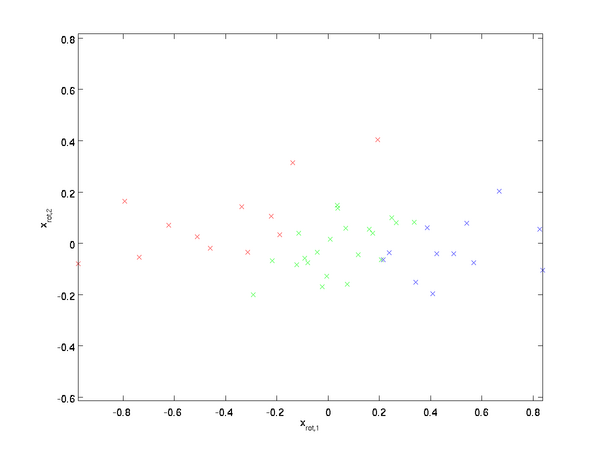
绘制出 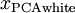 ，可以得到:

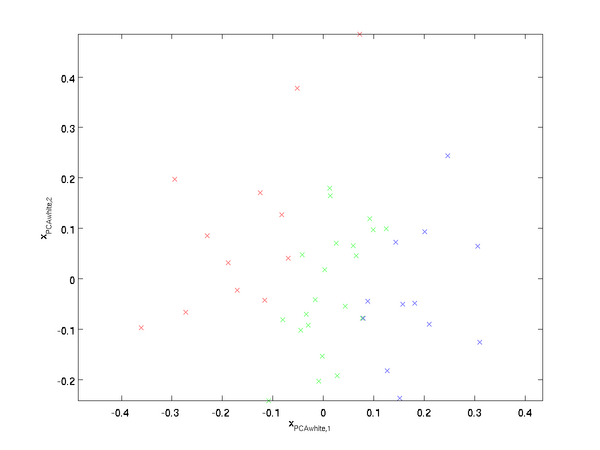
这些数据现在的协方差矩阵为单位矩阵 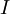 。 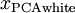是数据经过PCA白化后的版本:  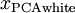中不同的特征之间不相关并且具有单位方差。

白化与降维相结合。 如果你想要得到经过白化后的数据，并且比初始输入维数更低,可以仅保留 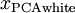 中前  个成分。当我们把PCA白化和正则化结合起来时(在稍后讨论)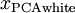， 中最后的少量成分将总是接近于0，因而舍弃这些成分不会带来很大的问题。

最后要说明的是，使数据的协方差矩阵变为单位矩阵 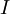 的方式并不唯一。具体地，如果  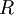是任意正交矩阵，即满足  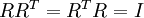(说它正交不太严格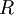， 可以是旋转或反射矩阵), 那么  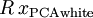仍然具有单位协方差。在ZCA白化中，令  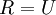。定义ZCA白化的结果为：

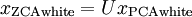
绘制 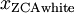，得到:

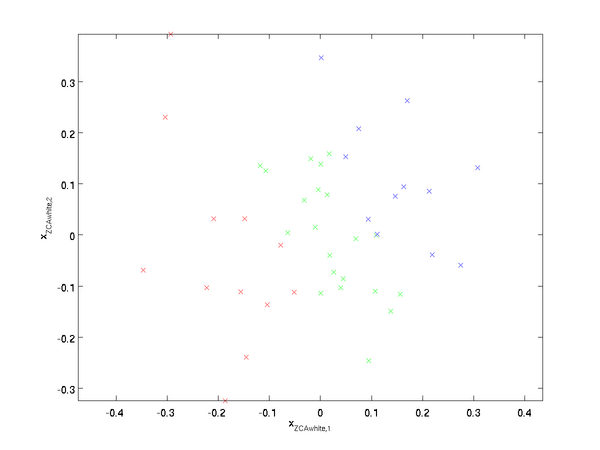
可以证明，对所有可能的 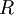，这种旋转使得  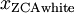尽可能地接近原始输入数据  。

当使用 ZCA白化时(不同于 PCA白化)，我们通常保留数据的全部 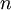 个维度，不尝试去降低它的维数。

实践中需要实现PCA白化或ZCA白化时，有时一些特征值 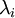 在数值上接近于0，这样在缩放步骤时我们除以  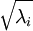将导致除以一个接近0的值；这可能使数据上溢 (赋为大数值)或造成数值不稳定。因而在实践中，我们使用少量的正则化实现这个缩放过程，即在取平方根和倒数之前给特征值加上一个很小的常数 ：

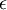当  在区间 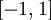 上时, 一般取值为 。

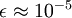对图像来说, 这里加上 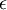 ，对输入图像也有一些平滑(或低通滤波)的作用。这样处理还能消除在图像的像素信息获取过程中产生的噪声，改善学习到的特征。