SDUST数据结构 - chap6 树与二叉树

判断题：

选择题：

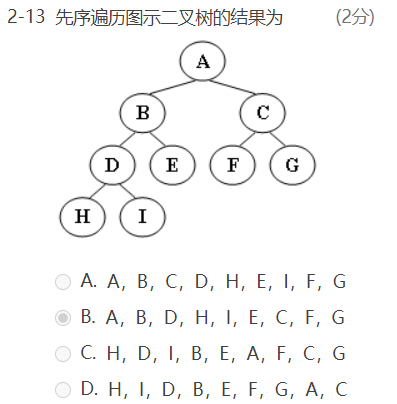
函数题：

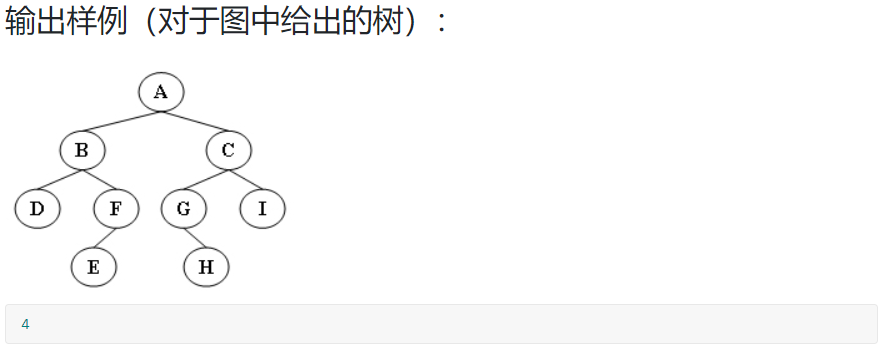
　　6-1 求二叉树高度：

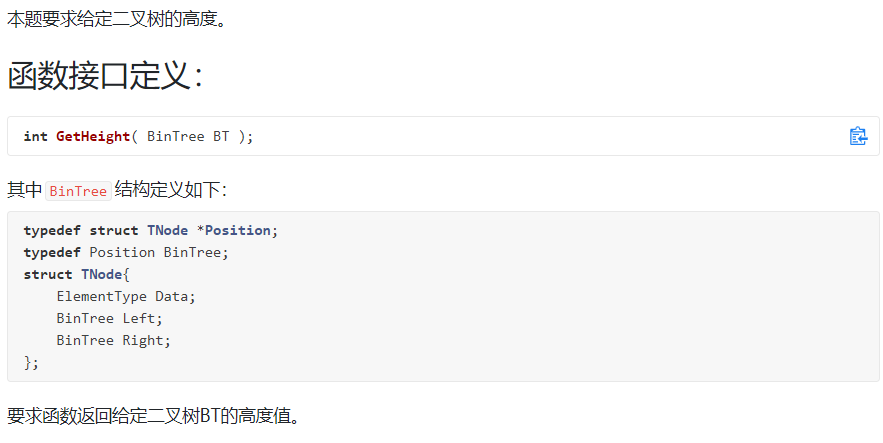
裁判测试程序样例：

#include <stdio.h>
#include <stdlib.h>

typedef char ElementType;
typedef struct TNode *Position;
typedef Position BinTree;
struct TNode{
    ElementType Data;
    BinTree Left;
    BinTree Right;
};

BinTree CreatBinTree(); /* 实现细节忽略 */
int GetHeight( BinTree BT );

int main()
{
    BinTree BT = CreatBinTree();
    printf("%d\n", GetHeight(BT));
    return 0;
}
/* 你的代码将被嵌在这里 */

代码：

int GetHeight(BinTree BT)
{
    if(BT == NULL)//判断是否为空
    return 0;
    int l,r;
    l=GetHeight(BT->Left);//递归
    r=GetHeight(BT->Right);
    return l>=r?l+1:r+1;
} 

　　6-2 二叉树的遍历：

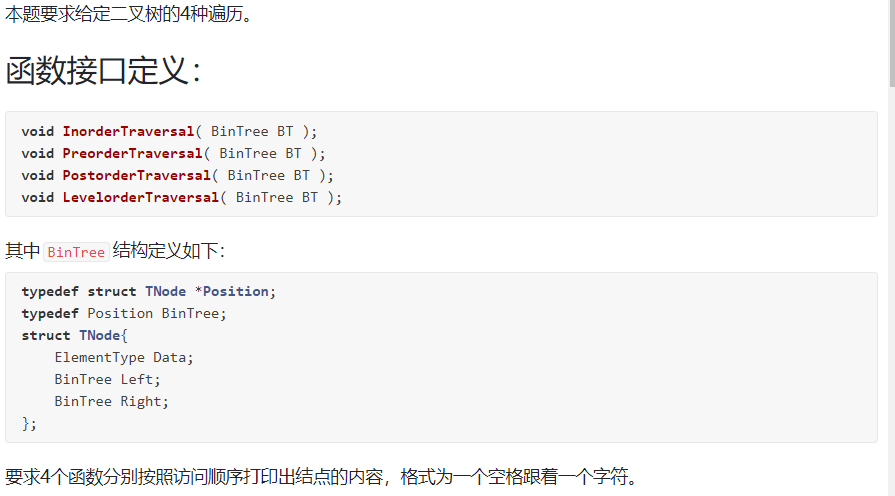
裁判测试程序样例：

#include <stdio.h>
#include <stdlib.h>

typedef char ElementType;
typedef struct TNode *Position;
typedef Position BinTree;
struct TNode{
    ElementType Data;
    BinTree Left;
    BinTree Right;
};

BinTree CreatBinTree(); /* 实现细节忽略 */
void InorderTraversal( BinTree BT );
void PreorderTraversal( BinTree BT );
void PostorderTraversal( BinTree BT );
void LevelorderTraversal( BinTree BT );

int main()
{
    BinTree BT = CreatBinTree();
    printf("Inorder:");    InorderTraversal(BT);    printf("\n");
    printf("Preorder:");   PreorderTraversal(BT);   printf("\n");
    printf("Postorder:");  PostorderTraversal(BT);  printf("\n");
    printf("Levelorder:"); LevelorderTraversal(BT); printf("\n");
    return 0;
}
/* 你的代码将被嵌在这里 */

代码：

void InorderTraversal( BinTree BT )//前三个依次递归，只需注意每一次的输出位置即可
{
    if(BT)
    {
        if(BT->Left)
            InorderTraversal(BT->Left);
        printf(" %c",BT->Data);
        if(BT->Right)
            InorderTraversal(BT->Right);
    }
}
void PreorderTraversal( BinTree BT )
{
    if(BT)
    {
        printf(" %c",BT->Data);
        if(BT->Left)
            PreorderTraversal(BT->Left);
        if(BT->Right)
            PreorderTraversal(BT->Right);
    }
}
void PostorderTraversal( BinTree BT )
{
    if (BT)
    {
        if (BT->Left)
             PostorderTraversal(BT->Left);
         if (BT->Right)
             PostorderTraversal(BT->Right);
         printf(" %c", BT->Data);
    }
}
void LevelorderTraversal( BinTree BT )
{
    BinTree bt[10001],root;
    int h=0,t=0;
    if(BT)
    {
        bt[t++]=BT;
        while(h!=t)
        {
            root=bt[h++];
            printf(" %c", root->Data);
            if(root->Left)
                bt[t++] = root->Left;
            if(root->Right)
                bt[t++] = root->Right;
        }
    }
}

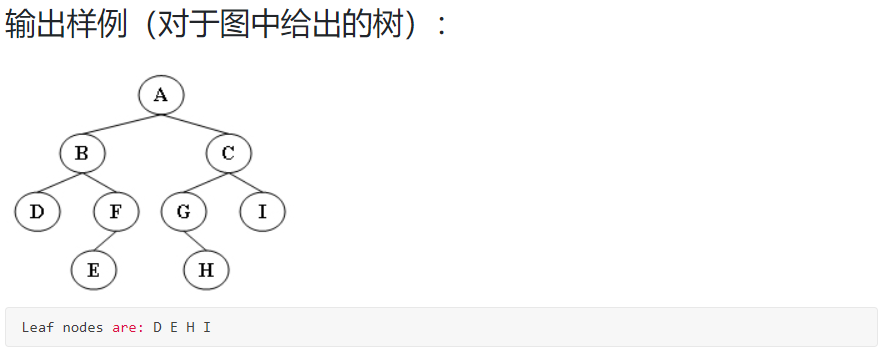
　　6-3 先序输出叶结点：

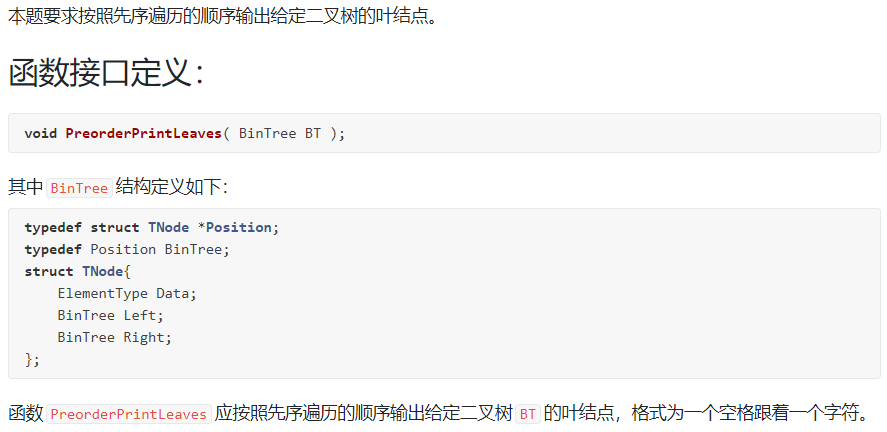
裁判测试程序样例：

#include <stdio.h>
#include <stdlib.h>

typedef char ElementType;
typedef struct TNode *Position;
typedef Position BinTree;
struct TNode{
    ElementType Data;
    BinTree Left;
    BinTree Right;
};

BinTree CreatBinTree(); /* 实现细节忽略 */
void PreorderPrintLeaves( BinTree BT );

int main()
{
    BinTree BT = CreatBinTree();
    printf("Leaf nodes are:");
    PreorderPrintLeaves(BT);
    printf("\n");

    return 0;
}
/* 你的代码将被嵌在这里 */

代码：

void PreorderPrintLeaves( BinTree BT )
{
    if(BT==NULL)//若为空，只退回当前函数
        return ;
    PreorderPrintLeaves(BT->Left);//递归调用
    PreorderPrintLeaves(BT->Right);
    if(BT->Left==NULL&&BT->Right==NULL)
        printf(" %c",BT->Data);
    //PreorderPrintLeaves(BT->Left);//递归调用
    //PreorderPrintLeaves(BT->Right);
}

　　7-1 根据后序和中序遍历输出先序遍历：

输入样例：

7
2 3 1 5 7 6 4
1 2 3 4 5 6 7

输出样例：

Preorder: 4 1 3 2 6 5 7

代码：

#include<bits/stdc++.h>
using namespace std;
typedef struct BiTNode
{
    int Data;
    struct BiTNode *lchild;
    struct BiTNode *rchild;
}BiTNode, *BiTree;
BiTree PlusTree(int *l, int *r, int n)
{
    if(n==0)
        return NULL;
    else
    {
        BiTree t=new BiTNode;
        t->Data=r[n-1];
        int i=0;
        for(i=0;i<n;i++)
        {
            if(r[n-1]==l[i])
                break;
        }
        t->lchild = PlusTree(l, r, i);
        t->rchild = PlusTree(l+i+1, r+i, n-i-1);
        return t;
    }
}
void PreorderTraversal(BiTree BT)
{
    if(BT == NULL)
        return;
    printf(" %d", BT->Data);
    PreorderTraversal(BT->lchild);
    PreorderTraversal(BT->rchild);
}
int main()
{
    int n;
    scanf("%d",&n);
    int a[35],b[35];
    for(int i=0;i<n;i++)
        cin>>b[i];
    for(int j=0;j<n;j++)
        cin>>a[j];
    BiTree tree;
    tree = PlusTree(a, b, n);
    printf("Preorder:");
    PreorderTraversal(tree);
    printf("\n");
    return 0;
}
 

　　7-2 树的同构：

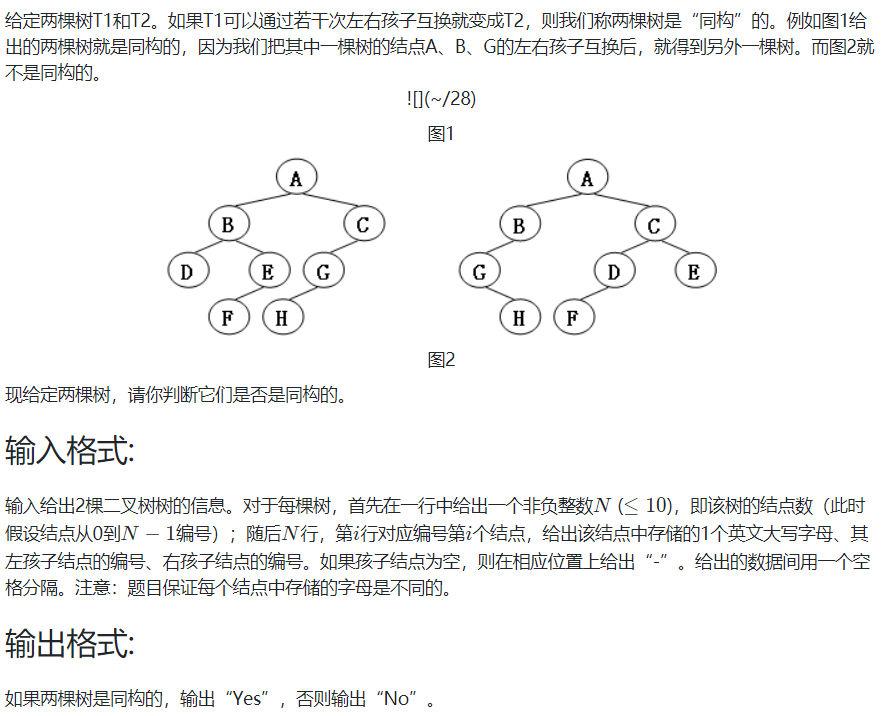
输入样例1：

8
A 1 2
B 3 4
C 5 -
D - -
E 6 -
G 7 -
F - -
H - -
8
G - 4
B 7 6
F - -
A 5 1
H - -
C 0 -
D - -
E 2 -

输出样例：

Yes

输入样例：

8
B 5 7
F - -
A 0 3
C 6 -
H - -
D - -
G 4 -
E 1 -
8
D 6 -
B 5 -
E - -
H - -
C 0 2
G - 3
F - -
A 1 4

输出样例：

No

代码：

#include<cstdio>
typedef int Tree;
struct TNode{
    Tree left, right;
    char data;
    int flag;
}T1[15], T2[15];
int flag[15];
Tree BuildTree( struct TNode T[]){
    Tree R=-1, cl, cr;
    int n;
    scanf("%d\n", &n);
    for(int i=0; i<n; i++)flag[i]=0;
    for(int i=0; i<n; i++){
        scanf("%c %c %c\n", &T[i].data, &cl, &cr);
        if(cl!='-'){
            T[i].left=cl - '0';
            flag[T[i].left]=1;
        }else{
            T[i].left=-1;
        }
        if(cr!='-'){
            T[i].right= cr-'0';
            flag[T[i].right]=1;
        }else{
            T[i].right=-1;
        }
    }
    for(int i=0; i<n; i++)
        if(flag[i]==0){
            R=i;
            break;
        }
    return R;
}
int PanDuan(Tree R1, Tree R2){
    if(R1==-1 && R2==-1)return 1;
    if((R1==-1 && R2!=-1) || (R2==-1 && R1!=-1))return 0;
    if(T1[R1].data!=T2[R2].data)return 0;
    if(T1[R1].left==-1 && T2[R2].left==-1)
        return PanDuan(T1[R1].right, T2[R2].right);
    if((T1[R1].left!=-1&&T2[R2].left!=-1)&&(T1[T1[R1].left].data==T2[T2[R2].left].data)){
        return(PanDuan(T1[R1].left, T2[R2].left)&&PanDuan(T1[R1].right, T2[R2].right));
    }else{
        return(PanDuan(T1[R1].right, T2[R2].left)&&PanDuan(T1[R1].left, T2[R2].right));
    }
}
int main(){
    Tree a, b;
    a=BuildTree(T1);
    b=BuildTree(T2);
    if(PanDuan(a, b)){
        printf("Yes");
    }else{
        printf("No");
    }
    return 0;
}

　　7-3 修理牧场：

输入样例：

8
4 5 1 2 1 3 1 1

输出样例：

49

代码：

#include<bits/stdc++.h>
using namespace std;
int main()
{
    int n;
    scanf("%d",&n);
    priority_queue<int, vector<int>, greater<int> > w;
    int a[n];
    int i=0;
    int sum=0;   //待求最小值
    for(;i<n;i++)
    {
        scanf("%d",&a[i]);
        w.push(a[i]);
    }
    int x;//存取现小顶堆
    int y;//存取新小顶堆
    while(!w.empty())    //最短的木头二合一
    {
        x=w.top();
        w.pop();       //用完移除

        if(w.empty())  //移除x后没有元素了，说明x是木头总长，不再循环
        {
            break;
        }
        y=w.top();
        w.pop();
        x+=y;
        sum+=x;
        w.push(x);   //新木头放入堆中
    }
    printf("%d",sum);
}

　　7-4 完全二叉搜索树：

输入样例：

10
1 2 3 4 5 6 7 8 9 0

输出样例：

6 3 8 1 5 7 9 0 2 4

代码：

#include<bits/stdc++.h>
using namespace std;
int n, flag;
int a[1001];
int b[1001];
void DFS(int aa)
{
    if(aa>n)
        return ;
    DFS(2*aa);
    b[aa]=++flag;
    DFS(2*aa+1);
}
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&a[i]);
    }
    sort(a+1, a+n+1);
    DFS(1);
    for(int i=1;i<=n;i++)
    {
        if(i==1)
            printf("%d",a[b[i]]);
        else
            printf(" %d",a[b[i]]);
    }
}