弗洛伊德算法（Floyd算法）

原博来自http://www.cnblogs.com/skywang12345/

弗洛伊德算法介绍

和Dijkstra算法一样，弗洛伊德(Floyd)算法也是一种用于寻找给定的加权图中顶点间最短路径的算法。该算法名称以创始人之一、1978年图灵奖获得者、斯坦福大学计算机科学系教授罗伯特·弗洛伊德命名。

基本思想

通过Floyd计算图G=(V,E)中各个顶点的最短路径时，需要引入一个矩阵S，矩阵S中的元素a[i][j]表示顶点i(第i个顶点)到顶点j(第j个顶点)的距离。

假设图G中顶点个数为N，则需要对矩阵S进行N次更新。初始时，矩阵S中顶点a[i][j]的距离为顶点i到顶点j的权值；如果i和j不相邻，则a[i][j]=∞。 接下来开始，对矩阵S进行N次更新。第1次更新时，如果"a[i][j]的距离" > "a[i][0]+a[0][j]"(a[i][0]+a[0][j]表示"i与j之间经过第1个顶点的距离")，则更新a[i][j]为"a[i][0]+a[0][j]"。 同理，第k次更新时，如果"a[i][j]的距离" > "a[i][k]+a[k][j]"，则更新a[i][j]为"a[i][k]+a[k][j]"。更新N次之后，操作完成！

单纯的看上面的理论可能比较难以理解，下面通过实例来对该算法进行说明。

弗洛伊德算法图解

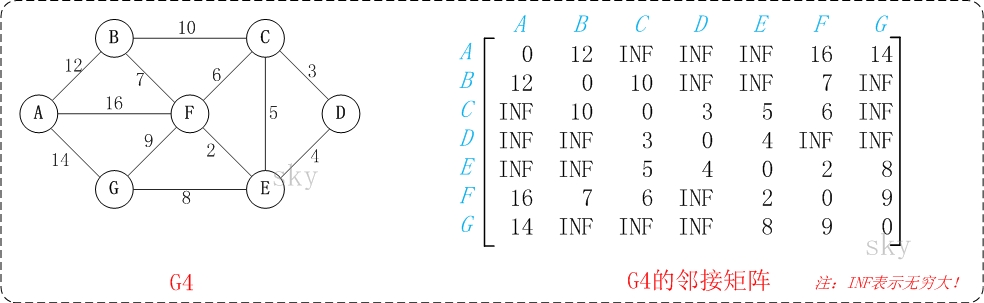
以上图G4为例，来对弗洛伊德进行算法演示。

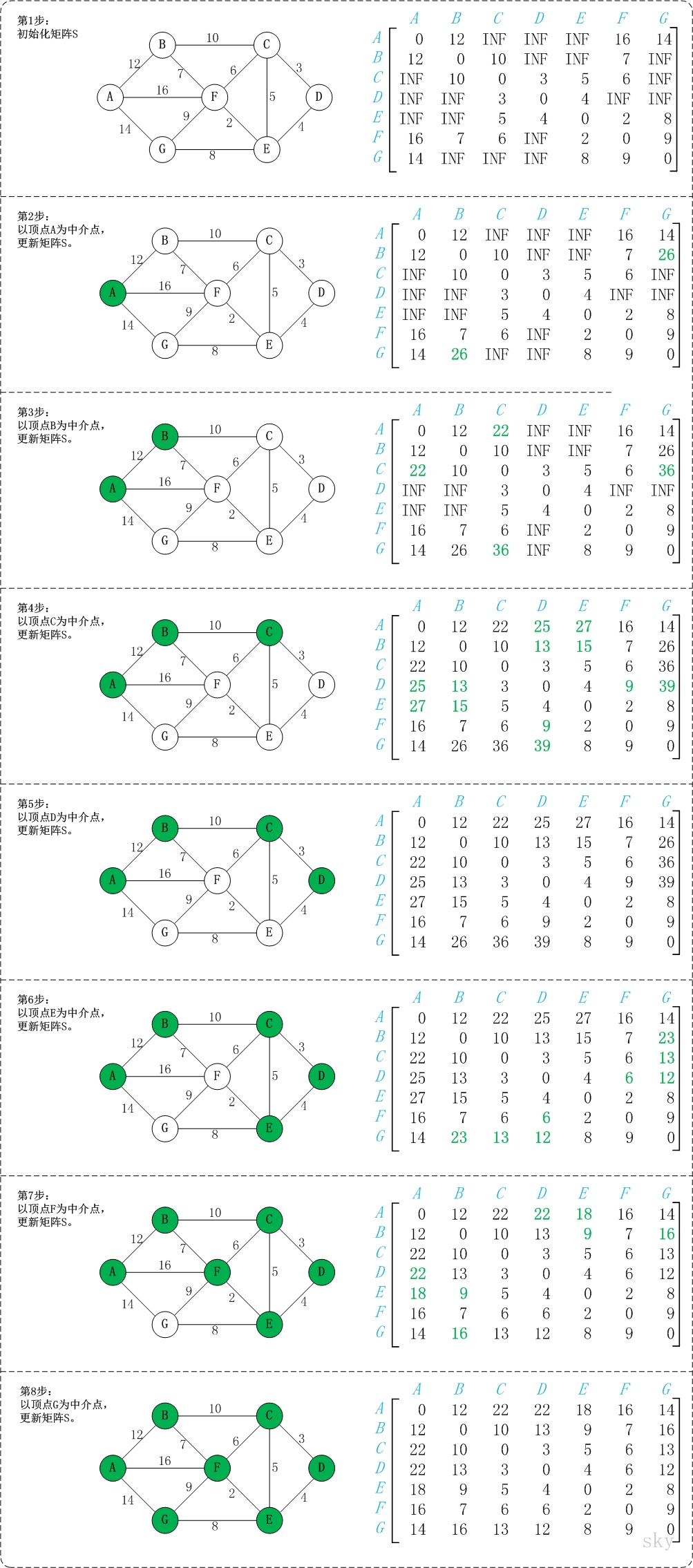
初始状态：S是记录各个顶点间最短路径的矩阵。 
第1步：初始化S。 
    矩阵S中顶点a[i][j]的距离为顶点i到顶点j的权值；如果i和j不相邻，则a[i][j]=∞。实际上，就是将图的原始矩阵复制到S中。 
    注:a[i][j]表示矩阵S中顶点i(第i个顶点)到顶点j(第j个顶点)的距离。

第2步：以顶点A(第1个顶点)为中介点，若a[i][j] > a[i][0]+a[0][j]，则设置a[i][j]=a[i][0]+a[0][j]。 
    以顶点a[1]6，上一步操作之后，a[1][6]=∞；而将A作为中介点时，(B,A)=12，(A,G)=14，因此B和G之间的距离可以更新为26。

同理，依次将顶点B,C,D,E,F,G作为中介点，并更新a[i][j]的大小。

弗洛伊德算法的代码说明

以"邻接矩阵"为例对弗洛伊德算法进行说明，对于"邻接表"实现的图在后面会给出相应的源码。

1. 基本定义

 // 邻接矩阵
 typedef struct _graph
 {
     char vexs[MAX];       // 顶点集合
     int vexnum;           // 顶点数
     int edgnum;           // 边数
     int matrix[MAX][MAX]; // 邻接矩阵
 }Graph, *PGraph;

Graph是邻接矩阵对应的结构体。 
vexs用于保存顶点，vexnum是顶点数，edgnum是边数；matrix则是用于保存矩阵信息的二维数组。例如，matrix[i][j]=1，则表示"顶点i(即vexs[i])"和"顶点j(即vexs[j])"是邻接点；matrix[i][j]=0，则表示它们不是邻接点。

2. 弗洛伊德算法

 /*
  * floyd最短路径。
  * 即，统计图中各个顶点间的最短路径。
  *
  * 参数说明：
  *        G -- 图
  *     path -- 路径。path[i][j]=k表示，"顶点i"到"顶点j"的最短路径会经过顶点k。
  *     dist -- 长度数组。即，dist[i][j]=sum表示，"顶点i"到"顶点j"的最短路径的长度是sum。
  */
 void floyd(Graph G, int path[][MAX], int dist[][MAX])
 {
     int i,j,k;
     int tmp;

     // 初始化
     for (i = ; i < G.vexnum; i++)
     {
         for (j = ; j < G.vexnum; j++)
         {
             dist[i][j] = G.matrix[i][j];    // "顶点i"到"顶点j"的路径长度为"i到j的权值"。
             path[i][j] = j;                 // "顶点i"到"顶点j"的最短路径是经过顶点j。
         }
     }

     // 计算最短路径
     for (k = ; k < G.vexnum; k++)
     {
         for (i = ; i < G.vexnum; i++)
         {
             for (j = ; j < G.vexnum; j++)
             {
                 // 如果经过下标为k顶点路径比原两点间路径更短，则更新dist[i][j]和path[i][j]
                 tmp = (dist[i][k]==INF || dist[k][j]==INF) ? INF : (dist[i][k] + dist[k][j]);
                 if (dist[i][j] > tmp)
                 {
                     // "i到j最短路径"对应的值设，为更小的一个(即经过k)
                     dist[i][j] = tmp;
                     // "i到j最短路径"对应的路径，经过k
                     path[i][j] = path[i][k];
                 }
             }
         }
     }

     // 打印floyd最短路径的结果
     printf("floyd: \n");
     for (i = ; i < G.vexnum; i++)
     {
         for (j = ; j < G.vexnum; j++)
             printf("%2d  ", dist[i][j]);
         printf("\n");
     }
 }

完整代码可以见：http://www.wutianqi.com/?p=1903