机器学习理论基础学习18---高斯过程回归(GPR)

一、高斯(分布)过程(随机过程)是什么？

一维高斯分布	多维高斯分布	无限维高斯分布
	高斯网络	高斯过程

简单的说，就是一系列关于连续域（时间或空间）的随机变量的联合，而且针对每一个时间或是空间点上的随机变量都是服从高斯分布的。

举个例子：倘若你人生的每一个时刻看做一个随机变量，且都是满足高斯分布，那么你的人生就可以看做一个高斯过程，既有很多确定的东西，确定的是mean和kernel，如你的人生中你起点决定的你人生的大致范围，又有极大地不确定性，本质还是随机变量的整体，就像你可以凭借自身的努力改变很多东西，这就是属于你的高斯过程。

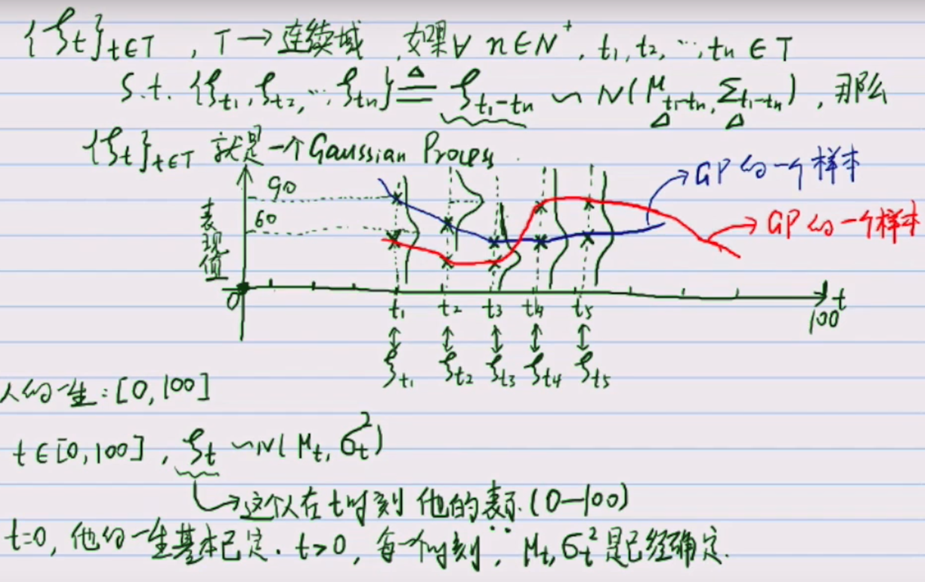
二、高斯过程有什么用？--->高斯过程回归

简单的说，由于它性质完美，计算简单，形式漂亮，所以可以被广泛应用在各种统计建模中，包括一些非线性的预测推断问题

1、weight-space角度

先来回顾贝叶斯线性回归(Bayesian Linear Regression)，分为两部分（1）Inference（2）预测

如果线性回归问题本身不是线性的，就要进行非线性转换，

2、weighted-space角度 ---> function-space 角度

3、function-space角度

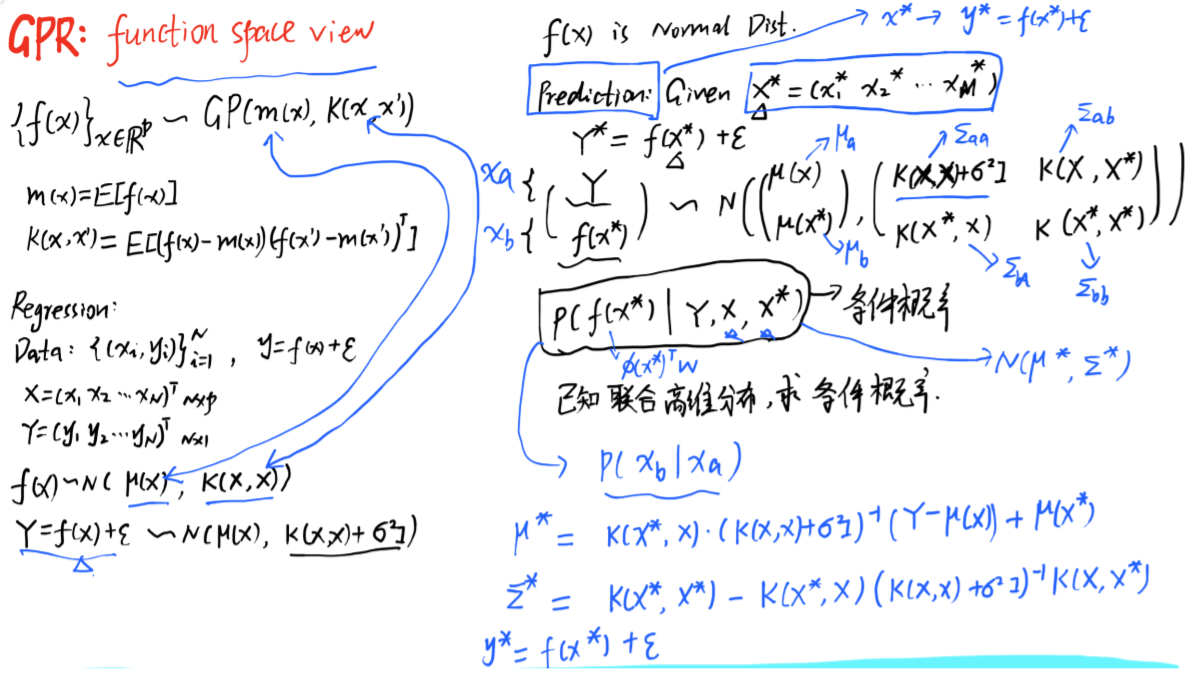
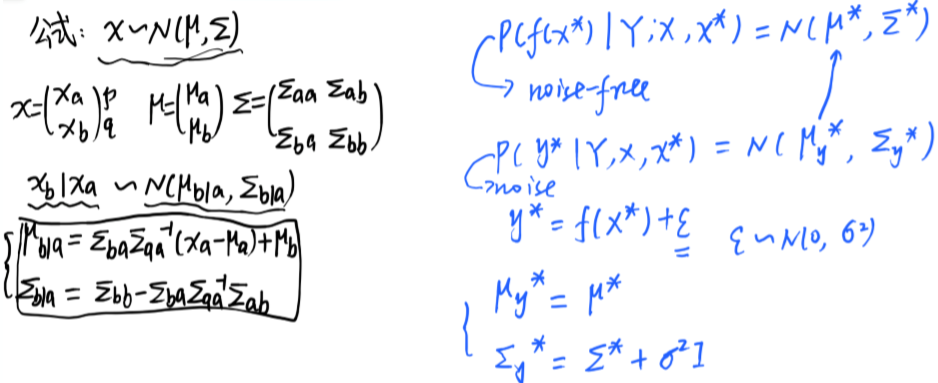
三、高斯过程回归怎么用？

因为高斯分布在自然界无比常见，所以把原来的n个y看成服从高斯分布，来了一个新的Xn+1，这n+1个y还是服从一个联合正态分布的。

已知n个点的(xa,ya)，想知道在任意一个新的点xb,对应的yb是怎么样的。可以用来进行贝叶斯优化。

     

其中,xa和xb,yb为观察到的值,ya为需要预测的值

要点：

1.简单来说，高斯过程可以看成是一个函数，函数的输入是x，函数的输出是高斯分布的均值和方差。

2.y的相关性取决于x，然后由x到y用高斯核函数表示其相关性

3.Y之间的分布用协方差矩阵表示

4、有噪声时把噪声加到对角线上

四、核函数如何选取？

对于上面的协方差矩阵K，其中k(x,y)表示核函数，那么这个核函数如选取？

1、高斯核函数

RBF（高斯核函数，也叫做径向基函数）

2、Matern核

参考文献：

【1】浅析高斯过程回归（Gaussian process regression）附代码

【2】高斯过程回归GPR

【3】浅谈高斯过程回归