算法问题实战策略 FENCE

地址 https://algospot.com/judge/problem/read/FENCE

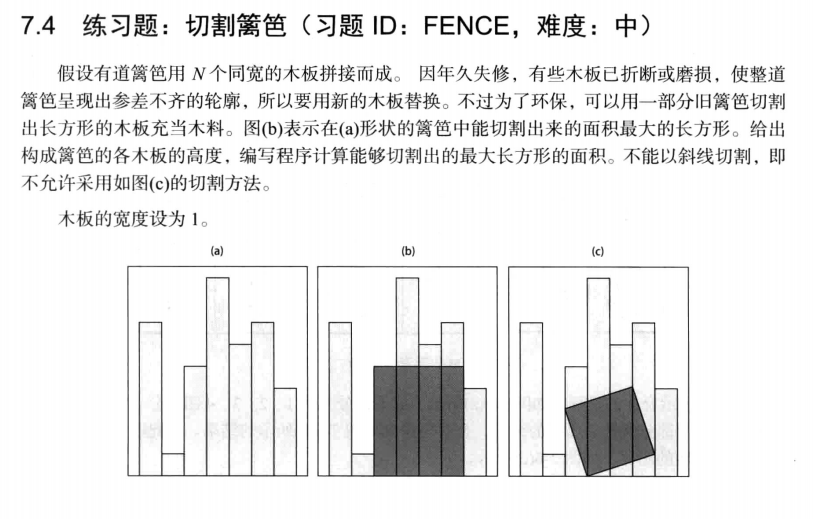
开始考虑暴力遍历

 #include <iostream>
 #include <string>
 #include <vector>
 #include <algorithm>

 using namespace std;

 int n;
 int m;

 vector<int> h;

 int func()
 {
     int ret = ;

     for (int i = ; i < h.size(); i++) {
         int minHeight = h[i];
         for (int j = i; j < h.size(); j++) {
             minHeight = min(minHeight,h[j]);
             ret = max(ret, (j - i + )*minHeight);
         }
     }

     return ret;
 }

 int main()
 {
     cin >> n;

     while (n--) {
         h.clear();
         m = ;
         cin >> m;

         for (int i = ; i < m; i++) {
             int t;
             cin >> t;
             h.push_back(t);
         }

         cout << func() << endl;
     }

     return ;
 }

后面优化 采取分冶的办法  最大值要么在左边 要么在右边 要么经过左右 三种情况。

左右两种情况采取递归的方式进行计算

穿越分界由左到右的情况则采用以下方法计算:

取中间两块木板 长方形长度为2 高度为两筐木板短的那块，然后向两边扩展，选取左边或者右边较高的那块木板扩展.每次扩展计算面积，记录当前最大面积。最后得到穿越分界由左到右的最大面积

之所以会取较高的木板扩展是因为面积要以最低的高度计算 如果两边扩展不取较高的而是取较低的木板 那么如果扩展的木板低于当前高度 会遗漏一些情况未计算面积 从而产生错误.

代码如下:

 #include <iostream>
 #include <string>
 #include <vector>
 #include <algorithm>

 using namespace std;

 int n;
 int m;
 vector<int> h;
 int solve(int left, int right)
 {
     if (left == right) return h[left];
     int mid = (left + right) / ;
     int ret = max(solve(left, mid), solve(mid + , right));

     int lo = mid, hi = mid + ;
     int height = min(h[lo], h[hi]);
     ret = max(ret, height * );
     while (left < lo || hi < right) {
         if (hi < right && (lo == left || h[lo - ] < h[hi + ])) {
             ++hi;
             height = min(height,h[hi]);
         }
         else {
             --lo;
             height = min(height,h[lo]);
         }
         ret = max(ret, height*(hi - lo + ));
     }
     return ret;
 }

 int main()
 {
     cin >> n;

     while (n--) {
         h.clear();
         m = ;
         cin >> m;
         for (int i = ; i < m; i++) {
             int t;
             cin >> t;
             h.push_back(t);
         }

         cout << solve( , m-) << endl;
     }

     return ;
 }