Noip 2016 愤怒的小鸟 题解

　　　　　　　[NOIP2016]愤怒的小鸟

　　　　　　　　　　　　　　　　　时间限制：1 s   内存限制：256 MB

【题目描述】

Kiana最近沉迷于一款神奇的游戏无法自拔。

简单来说，这款游戏是在一个平面上进行的。

有一架弹弓位于(0,0)处，每次Kiana可以用它向第一象限发射一只红色的小鸟，小鸟们的飞行轨迹均为形如y = ax^2 + bx的曲线，其中a, b是Kiana指定的参数，且必须满足a<0。

当小鸟落回地面(即x轴)时，它就会瞬间消失。

在游戏的某个关卡里，平面的第一象限中有n只绿色的小猪，其中第i只小猪所在的坐标为(xi,yi)。

如果某只小鸟的飞行轨迹经过了(xi,yi)，那么第i只小猪就会被消灭掉，同时小鸟将会沿着原先的轨迹继续飞行;

如果一只小鸟的飞行轨迹没有经过(xi,yi)，那么这只小鸟飞行的全过程就不会对第i只小猪产生任何影响。

例如，若两只小猪分别位于(1, 3 )和(3, 3 )

Kiana可以选择发射一只飞行轨迹为y=-x^2+ 4x的小鸟，这样两只小猪就会被这只小鸟一起消灭。

而这个游戏的目的，就是通过发射小鸟消灭所有的小猪。

这款神奇游戏的每个关卡对Kiana来说都很难，所以Kiana还输入了一些神秘的指令，使得自己能更轻松地完成这个游戏。这些指令将在【输入格式】中详述。

假设这款游戏一共有T个关卡，现在Kiana想知道，对于每一个关卡，至少需要发射多少只小鸟才能消灭所有的小猪。由于她不会算，所以希望由你告诉她。

【输出格式】

输出到文件angrybirds.out中。

对每个关卡依次输出一行答案。

输出的每一行包含一个正整数，表示相应的关卡中，消灭所有小猪最少需要的小鸟数量。

【样例1输入】

2
2 0
1.00 3.00
3.00 3.00
5 2
1.00 5.00
2.00 8.00
3.00 9.00
4.00 8.00
5.00 5.00

【样例1输出】

1
1

【提示1】

这组数据中一共有两个关卡。 第一个关卡与【问题描述】中的情形相同，2只小猪分别位于((1.00, 3.00)和(3.00, 3.00)，只需发射一只飞行轨迹为y = -x2 + 4x的小鸟即可消灭它们。 第二个关卡中有5只小猪，但经过观察我们可以发现它们的坐标都在抛物线y=-x^2+ 6x上，故Kiana只需要发射一只小鸟即可消灭所有小猪。

【样例2输入】

3
2 0
1.41 2.00
1.73 3.00
3 0
1.11 1.41
2.34 1.79
2.98 1.49
5 0
2.72 2.72
2.72 3.14
3.14 2.72
3.14 3.14
5.00 5.00

【样例2输出】

2
2
3

【样例3输入】

1
10 0
7.16 6.28
2.02 0.38
8.33 7.78
7.68 2.09
7.46 7.86
5.77 7.44
8.24 6.72
4.42 5.11
5.42 7.79
8.15 4.99

【样例3输出】

6

【提示】

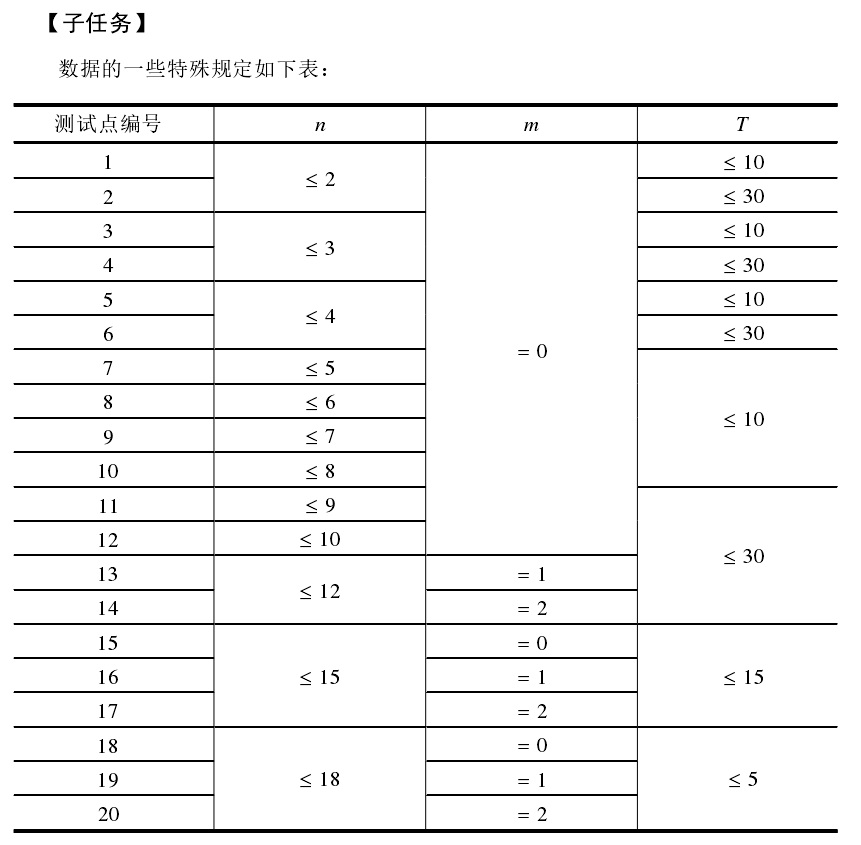
　　难得今天不考试，找几道前几年的NOIP题重新打一下测一下能力。

　　这道题还是挺满意的，过编译，过样例1A，一开始想到的是O(n^2)预处理加O(2^n*n^2)的打法，算着超时，然后就看了一下剪枝，却发现这样貌似不加剪枝也能过。

　　这道题数据范围这么小，应该是搜索或者状压，对于状压，状态数组就是f[i]表示把猪打到状态i所花费的最小代价，那么，我们每在这个基础上新打一个猪在大多数情况下可以再多带走一个的，我们可以n^2预处理出来如果我们一次性带走两头指定的猪实际能带走那些猪，然后转移就是f[i|link[j][k]]=min(f[i]+1,f[i|link[j][k]])，还是比较容易的，只是要注意，link是保留字，以及烦人的精度问题。

#include <iostream>
#include <cstdlib>
#include <cstdio>
#include <cstring>
#include <queue>
#include <algorithm>
#include <cmath>
#include <map>
using namespace std;
int T,n,m;
double x[20],y[20];
int lin[20][20],f[1<<18];
void init(int aa,int bb)
{
	if(fabs(x[aa]-x[bb])-0.0000001<0.0)return;
	double x1=x[aa],x2=x[bb],y1=y[aa],y2=y[bb];
	double b=(y2*x1*x1-x2*x2*y1)/(x1*x1*x2-x1*x2*x2);
	double a=(y1-b*x1)/(x1*x1);
	if(a-0.00000001<0.0&&fabs(a)-0.0000001>0)
	{
		lin[aa][bb]=(1<<(aa-1))|(1<<(bb-1));
		for(int i=1;i<=n;i++)
		{
			if(i==aa||i==bb)continue;
			if(abs(a*x[i]*x[i]+b*x[i]-y[i])-0.0000001<0.0)
			{

				lin[aa][bb]|=(1<<(i-1));
			}
		}

	}
}
int main()
{
	scanf("%d",&T);
while(T--)
{
	memset(lin,0,sizeof(lin));
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++)
	{
		scanf("%lf%lf",&x[i],&y[i]);
	}
	for(int i=1;i<=n;i++)
	{
		for(int j=i+1;j<=n;j++)
		{
			init(i,j);
		}
	}
	memset(f,0xf,sizeof(f));
	f[0]=0;
	for(int i=0;i<(1<<n);i++)
	{	

		for(int j=1;j<=n;j++)
		{
			if((i&(1<<(j-1)))==0)
			{
				f[i|(1<<(j-1))]=min(f[i]+1,f[i|(1<<(j-1))]);
				for(int k=j+1;k<=n;k++)
				{
					if(lin[j][k])
					{
						f[i|lin[j][k]]=min(f[i]+1,f[i|lin[j][k]]);
					}
				}
			}
		}
	}
	printf("%d\n",f[(1<<n)-1]);
}
	return 0;
}