npmrc npm配置文件
一、全局
这个文件在全局会放在/users/${yourname}/.npmrc
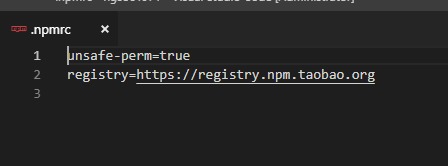
里面最重要的是registry,npm的源
二、项目
项目里面如果和package.json同级存放了这个.npmrc
那么就可以实现,仅仅对于这个项目,换npm的源了
npmrc npm配置文件的更多相关文章
- NPM 配置文件修改
NPM 配置文件修改 几乎每一门语言都有配套的包管理器,比如 Ruby 有 RubyGems,Go 有 go modules,npm 作为 node 的包管理器,你有想过全局安装的 node 包都放在 ...
- npm配置文件
npm获取配置的方式,优先级由高到底. 命令行参数. 以设置代理为例:--proxy http://server:port即将proxy的值设为http://server:port. 环境变量. 以n ...
- 构建纯TypeScript应用
构建纯TypeScript应用 现在只有命令行应用的例子. 前言 现在,应用开发的趋势是命令行接口应用和Web应用. node.js 和 typescript的崛起所以,这里讨论如何创建纯的TypeS ...
- 了解npm的文件结构(npm-folders)和配置文件(npm-mrc)
一.npm的文件结构 npm的安装: 本地安装 1. 将安装包放在 ./node_modules 下(运行 npm 命令时所在的目录),如果没有 node_modules 目录,会在当前执行 npm ...
- Node.js npm 详解
一.npm简介 安装npm请阅读我之前的文章Hello Node中npm安装那一部分,不过只介绍了linux平台,如果是其它平台,有前辈写了更加详细的介绍. npm的全称:Node Package M ...
- npm换源
作者一介布衣:http://yijiebuyi.com/blog/b12eac891cdc5f0dff127ae18dc386d4.html npm 是node.js 环境下的包管理器,非常强大智能. ...
- NPM使用详解(上)
1.NPM是什么? NPM是JavaScript的包管理工具,在安装NodeJS(什么?你不知道node?来,我们合计合计:https://nodejs.org/)的时候,会自动安装上npm. 要查看 ...
- npm 国内镜像资源 --转载
npm 是node.js 环境下的包管理器,非常强大智能. 生活这这片神奇的土地上,各种奇葩手段屡见不鲜啊. 为什么要换源? npm 官方站点 http://www.npmjs.org/ 并没有被墙, ...
- NPM使用技巧
如果你是一个JavaScript系的开发者,一定不会陌生NPM,它既是一个平台,也是一个工具.在这个平台上,我们能够使用其他开发者提供的功能代码,当然我们也能将我们自己代码提交到这里分享给世界上的开发 ...
随机推荐
- Java之视频读取IO流解帧实施方案
获取视频处理对象的方式有很多,读取本地文件.读取url.读取摄像头等,而直接读流解析视频的实施方案却难以寻觅.此处有两种方案处理视频流(此处设定场景为用户上传视频,同时两种方式均需服务端安装ffmpe ...
- MD5进行解密操作
package com.dyy.test; import java.security.MessageDigest; public class TestMD5Util { /*** * MD5加码 生成 ...
- 为什么Elasticsearch查询变得这么慢了?
参考内容:https://mp.weixin.qq.com/s/RTpBaFpNELQCO6VE0KMfsw
- 初略 异步IO
import asyncio asyncio.coroutine() from concurrent.futures import ThreadPoolExecutor def task(): pri ...
- FPGA时序分析相关
什么叫时序? 时间与动作的相互关系,什么时间干什么活. 同步时序:单一时钟源,所有寄存器在单一时钟源下同步工作. 异步时序:多个时钟源,除使用带时钟的触发器之外,还可以使用不带时钟的触发器与延时元件作 ...
- shopNC 拓扑图
shopNC :
- 自学华为IoT物联网之路
自学华为IoT物联网之路 01 自学华为IoT物联网_01 物联网概述 02 自学华为IoT物联网_02 常见物联网通信技术 03 自学华为IoT物联网_03 公共事业物联网常见问题及解决方案 04 ...
- CCCC 喊山
2016年天梯赛模拟&初赛题集(nwu) 编程题30小题,共计580分 580分 编程题 5-14 喊山 (30分) 喊山,是人双手围在嘴边成喇叭状,对着远方高山发出“喂—喂喂—喂喂喂…… ...
- bzoj1014 火星人 (hash+splay+二分答案)
求公共前缀的问题可以用hash+二分来解决,但这个是动态的,所以我们用平衡树来维护区间的hash值 复杂度$O(mlog^2n)$ #include<bits/stdc++.h> #def ...
- base64加密图片处理
场景:下载html中内嵌的base64加密图片 举个例子,博客园的插入图片有两种方式,一是引用图片链接,二是直接粘贴2进制图片文件.以第二种方式的图片则是以base64加密的方式内嵌在html页面中. ...
