洛谷CF264D Colorful Stones（子序列匹配，思维）

洛谷题目传送门

神仙思维题。

对于两个字符串的匹配问题，似乎之前蒟蒻写的HAOI2010最长公共子序列题解中提到的建网格图模型是一种套路？

给一个稍微强一点的样例（把字母换成了ABC）

AABCB
BACBA

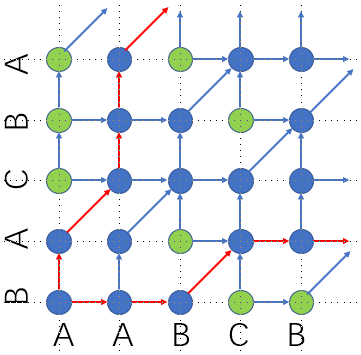
它所对应的网格图如下（横轴代表\(s\)，纵轴代表\(t\)，显示的点表示可达状态）

我们首先可以大致确定，所有的可达状态在一个不规则图形的界内

（红色线条）。第\(i\)行（或列）的界是\([l_i,r_i]\)，而且类似two pointers，\(l_i\)和\(r_i\)都随\(i\)单调不降。拐角的顶点\((x,y)\)出现在前缀\(s_x\)和前缀\(t_y\)第一次匹配到其中一个是另一个的子序列的地方。

那么是不是这个界里面的状态都可达呢？显然不是，我们还可以看到这样的位置（中间有三个）：如果\(s_x=t_{y-1}\neq s_{x-1}=t_y\)的话，\((x,y)\)也会不可达。对应的两个子串形如AB和BA，蒟蒻接下来把该状态记作AB-BA。

仔细观察一下（或者打个表），除了这种情况，还有没有别的情况也是在界内却不可达的？貌似找不到啊。。。。。。

实际上，我们大概可以证明，在这个界内有且仅有AB-BA状态不可达。

图中的若干有向边从前驱节点指向后继节点。显然如果一个状态不可达，那么要么它没有前驱，要么它的所有前驱都不可达。

首先，一个节点没有前驱的情况就只有AB-BA那一种。当\(s_x=t_y\)时，我们可以肯定\((x,y)\)有前驱，随手画画就可以发现。

于是现在我们就需要证明，如果一个点不可达，那么它一定没有前驱，而不会出现它有前驱且前驱不可达。反证法，我们现在开始判定一个在界内的有前驱的节点\((x,y)\)，并假设它和它的前驱都不可达。

1. 它的前驱中有一个是\((x-1,y-1)\)。刚刚已经得出\((x-1,y-1)\)有前驱，那么我们又需要假设\((x-1,y-1)\)的前驱不可达。
2. 它的前驱中没有\((x-1,y-1)\)。则它的前驱可能有\((x-1,y)\)、\((x,y-1)\)。如果\((x-1,y)\)有前驱，那么我们又需要假设\((x-1,y)\)的前驱不可达；如果\((x-1,y)\)没有前驱，那么说明出现了AB-BA状态，则一定会有\((x-1,y-1)\)到\((x,y)\)的边，不符合设定。对\((x,y-1)\)的讨论同理。

于是，我们如果要假设某个点的所有前驱都不可达，我们必须假设它的某一个前驱的所有前驱都不可达，接着是前驱的前驱的前驱。。。。。。这个过程中\(x,y\)在递减，而最终\((x,y)\)到了边界上。显然边界上的点都是可达状态（从\((0,0)\)出发形成一条轮廓状路径），于是所有的假设都被推翻了。

思路清晰了以后，代码就简单了，只需要注意些细节。动态匹配子序列，维护\(l,r\)，还有对不同的状态记前缀和，这些都没什么好说的了。

#include<bits/stdc++.h>
#define RG register
#define R RG int
using namespace std;
const int N=1e6+9;
char s[N],t[N];
int f[N][8];
int main(){
    R n=0,m=0,x,y,l=0,r=0;
    RG long long ans=0;
    scanf("%s%s",s,t);
    for(n=0;s[n];++n)s[n]%=3;//只是凑巧发现RBG%3的余数不一样
    for(m=0;t[m];++m)t[m]%=3;
    for(x=1;x<n;++x){
        memcpy(f[x],f[x-1],32);//前缀和
        if(s[x-1]!=s[x])
            ++f[x][(s[x-1]>s[x])*4+s[x-1]+s[x]];
    }
    memcpy(f[n],f[n-1],32);
    for(y=0;y<m;++y){
        if(y&&t[y-1]!=t[y]){//注意边界
            x=(t[y-1]<t[y])*4+t[y-1]+t[y];
            ans-=f[r][x]-f[l][x];
        }
        while(r<n&&s[r]!=t[y])++r;
        ans+=r-l+1-(r==n);//同样注意边界
        if(r<n)++r;
        if(l<r&&s[l]==t[y])++l;
    }
    cout<<ans<<endl;
    return 0;
}