聚类——KFCM

聚类——认识KFCM算法

作者：凯鲁嘎吉 - 博客园 http://www.cnblogs.com/kailugaji/

一、KFCM概述

KFCM：基于核的改进的模糊c均值聚类算法。它是通过核函数将原始空间中的点映射到特征空间中，考虑到原始空间中的点无法用一个线性函数进行划分，于是将其变换到一个更高维度的空间中，可以在这个高维空间中找到一个线性函数，容易对原始数据进行划分。这个高维空间就叫特征空间。从低维到高维空间的映射函数的内积就叫核函数。将核函数引入机器学习的一个重要原因是：当特征空间维数很高而核函数计算量较之特征空间内的内积运算计算量相对很小时，这样做可以提高计算效率。

基于目标函数的FCM聚类算法存在两大缺陷:一方面，隶属度和为1的约束条件易造成它对对孤立点和噪声敏感;另一方面它本身是一种迭代下降的算法，使得它初始聚类中心敏感且不易收敛于全局最优。KFCM算法提高了聚类性能，使算法对噪声和孤立点具有较好的鲁棒性。

核函数的定义如下：

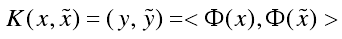
通过核函数改变模糊c均值聚类算法中的距离函数，定义如下目标函数:

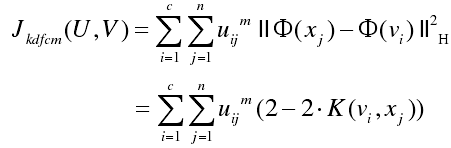
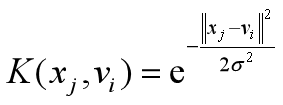
利用拉格朗日的极值必要条件，推出U ,V的迭代式如下:

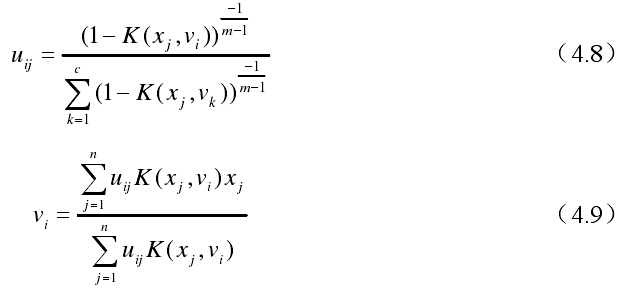
二、算法的步骤

这种方法通过核函数形成一种映射关系，将原始空间中的点转换到特征空间进行计算与分析，最后得到原始空间的最优划分。将上述基于核的模糊C均值聚类算法记为KFCM。