hdu4328(经典dp用悬线法求最大子矩形)

http://wenku.baidu.com/view/728cd5126edb6f1aff001fbb.html 关于悬线法，这里面有详解。

我当时只想到了记录最大长度，却没有想到如果连最左边和最右边的位置都记录的话这题就可以解决了。 学习了一种新算法很开心。

Cut the cake

Time Limit: 6000/3000 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 881    Accepted Submission(s): 328

Problem Description

Mark bought a huge cake, because his friend ray_sun’s birthday is coming. Mark is worried about how to divide the cake since it’s so huge and ray_sun is so strange. Ray_sun is a nut, you can never imagine how strange he was, is, and going to be. He does not eat rice, moves like a cat, sleeps during work and plays games when the rest of the world are sleeping……It is not a surprise when he has some special requirements for the cake. A considering guy as Mark is, he will never let ray_sun down. However, he does have trouble fulfilling ray_sun’s wish this time; could you please give him a hand by solving the following problem for him?
  The cake can be divided into n*m blocks. Each block is colored either in blue or red. Ray_sun will only eat a piece (consisting of several blocks) with special shape and color. First, the shape of the piece should be a rectangle. Second, the color of blocks in the piece should be the same or red-and-blue crisscross. The so called ‘red-and-blue crisscross’ is demonstrated in the following picture. Could you please help Mark to find out the piece with maximum perimeter that satisfies ray_sun’s requirements?

 

Input

The first line contains a single integer T (T <= 20), the number of test cases.
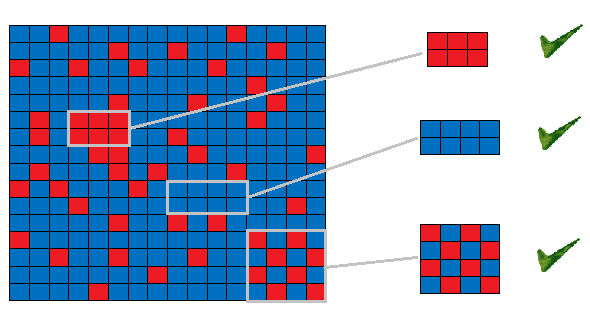
  For each case, there are two given integers, n, m, (1 <= n, m <= 1000) denoting the dimension of the cake. Following the two integers, there is a n*m matrix where character B stands for blue, R red.

 

Output

For each test case, output the cased number in a format stated below, followed by the maximum perimeter you can find.

 

Sample Input

2
1 1
B
3 3
BBR
RBB
BBB

 

Sample Output

Case #1: 4
Case #2: 8

 

Author

BJTU

 

Source

2012 Multi-University Training Contest 3

 

Recommend

zhoujiaqi2010   |   We have carefully selected several similar problems for you:  4321 4366 4335 4377 4371 

 

#include <iostream>
#include <string.h>
#include <stdio.h>
#include <algorithm>
using namespace std;
#define N 1010
 
//最大权子矩阵
int n,m;
int dp[N][N]; //记录每个点可以往上到达的最远距离
int dpl[N][N]; //记录这个点往左最远走多远
int dpr[N][N]; //
char g[N][N];
int ans=;
int    tmpl[N],tmpr[N];
 
void fuc(char key)
{
    memset(dp,,sizeof(dp));
    memset(dpl,,sizeof(dpl));
    memset(dpr,,sizeof(dpr));
    int mx=;
    for(int i=;i<=m;i++)
    {
        dpl[][i]=;
        dpr[][i]=m;
    }
 
    for(int i=;i<=n;i++)
    {
        int tmp=;
        for(int j=;j<=m;j++)
        {
            if(g[i][j]!=key)
            {
                tmp=j+;
            }
            else
            {
                tmpl[j]=tmp;
            }
        }
        tmp=m;
        for(int j=m;j>=;j--)
        {
            if(g[i][j]!=key)
            {
                tmp=j-;
            }
            else tmpr[j]=tmp;
        }
        //记录好了一个点能到达的最左边和最右边,接下来就是dp了
        for(int j=;j<=m;j++)
        {
            if(g[i][j]!=key)
            {
                dp[i][j]=;//最长为0
                dpl[i][j]=; dpr[i][j]=m;
                continue;
            }
            dp[i][j]=dp[i-][j]+;
            dpl[i][j]=max(dpl[i-][j],tmpl[j]);
            dpr[i][j]=min(dpr[i-][j],tmpr[j]);
            mx=max(*(dpr[i][j]-dpl[i][j]++dp[i][j]),mx);
        }
    }
    ans=max(ans,mx);
}
 
int main()
{
    int T;
    int tt=;
    scanf("%d",&T);
    while(T--)
    {
        ans=;
        scanf("%d%d",&n,&m);
        for(int i=;i<=n;i++)
            scanf("%s",g[i]+);
        fuc('B');
        fuc('R');
        for(int i=;i<=n;i++)
            for(int j=;j<=m;j++)
            {
                if( (i+j)%== )
                {
                    if(g[i][j]=='B') g[i][j]='R';
                    else g[i][j]='B';
                }
            }
        //想的还是比较清晰的...
 
        fuc('B');
        fuc('R');
        printf("Case #%d: ",tt++);
        printf("%d\n",ans);
    }
    return ;
}