操作系统（Day2.5）

一.为何要有操作系统

　　现代的计算机系统主要是由一个或者多个处理器，主存，硬盘，键盘，鼠标，显示器，打印机，网络接口及其他输入输出设备组成。

　　程序员无法把所有的硬件操作细节都了解到，管理这些硬件并且加以优化使用是非常繁琐的工作，这个繁琐的工作就是操作系统来干的，有了他，程序员就从这些繁琐的工作中解脱了出来，只需要考虑自己的应用软件的编写就可以了，应用软件直接使用操作系统提供的功能来间接使用硬件。

　　一句话来说，操作系统就是一个协调、管理和控制计算机硬件资源和软件资源的控制程序

二.操作系统的位置

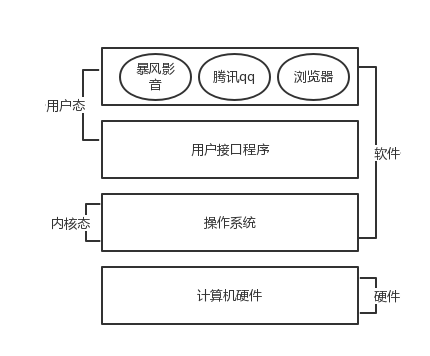
操作系统位于应用软件与计算机硬件之间，本质也是一个软件。操作系统由操作系统的内核（运行于内核，管理硬件资源）以及系统调用（运行于用户态，为应用程序猿写的应用程序提供调用接口），两部分组成。所以，单纯的讲，操作系统是运行于内核态的，是不太准确的

在详细一点就这样说，操作系统应该分成两部分功能：

　　1.隐藏了丑陋的硬件调用接口，为应用程序员提供调用硬件资源的更好，更简单，更清晰的模型（系统调用接口）。应用程序员有了这些接口后，就不用再考虑操作硬件的细节，专心开发自己的应用程序即可。

　　2.将应用程序对硬件资源的竞态请求变得有序化

三.操作系统的功能

　　　　操作系统就是一个协调、管理和控制计算机硬件资源和软件资源的控制程序。

　　操作系统与普通软件的区别：

　　　　操作系统由硬件保护，不能被用户修改。

　　　　操作系统是一个大型，复杂，长寿的软件。

　　操作系统的两大作用：

　　作用一：为应用程序提供如何使用硬件资源的抽象

　　作用二：管理硬件资源

四.操作系统的发展

1.第一代计算机(1940~1955)：真空管和穿孔卡片

特点：没有操作系统的概念

　　　所以的程序设计都是直接操控硬件

　　优点：

程序员在申请的时间段内独享整个资源，可以即时地调试自己的程序（有bug可以立刻处理）

　　缺点：

浪费计算机资源，一个时间段内只有一个人用。

2.第二代计算机（1955~1965）：晶体管和批处理系统

特点：有了操作系统概念；有了程序设计语言：FORTRAN语言或汇编语言，写到纸上，然后穿孔打成卡片，再讲卡片盒带到输入室，交给操作员，然后喝着咖啡等待输出接口

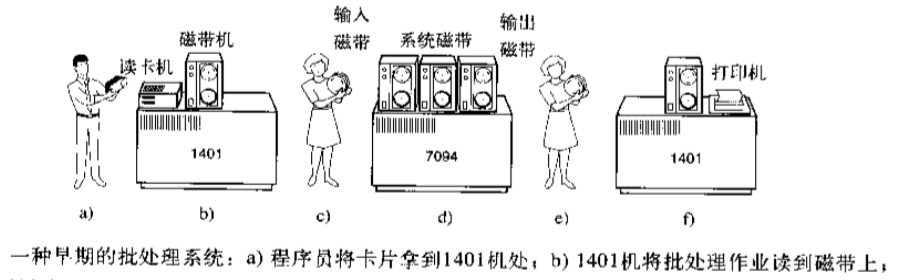
　　优点：

批处理，节省了机时

　　缺点：
（1）.整个流程需要人参与控制，将磁带搬来搬去（中间俩小人）

（2）.计算的过程仍然是顺序计算-》串行

（3）.程序员原来独享一段时间的计算机，现在必须被统一规划到一批作业中，等待结果和重新调试的过程都需要等同批次的其他程序都运作完才可以（这极大的影响了程序的开发效率，无法及时调试程序）

3.第三代计算机（1965~1980）：集成电路芯片和多道程序设计

第三代计算机的操作系统广泛应用了第二代计算机的操作系统没有的关键技术：多道技术

cpu在执行一个任务的过程中，若需要操作硬盘，则发送操作硬盘的指令，指令一旦发出，硬盘上的机械手臂滑动读取数据到内存中，这一段时间，cpu需要等待，时间可能很短，但对于cpu来说已经很长很长，长到可以让cpu做很多其他的任务，如果我们让cpu在这段时间内切换到去做其他的任务，这样cpu不就充分利用了吗。这正是多道技术产生的技术背景

　　多道技术：（多道指的是多道/个程序）

　　3.1.空间上的复用：内存中进入多个程序（ps:内存必须实现物理级别的隔离）

　　3.2.时间上的复用：CPU要切换

　　一个程序占用cpu的时间太长

　　一个程序遇到了I/O阻塞

4.第四代计算机：（1980~至今）：个人计算机