0-1背包问题与N皇后问题的纠结

昨日同学要我帮他看一道算法，如下：

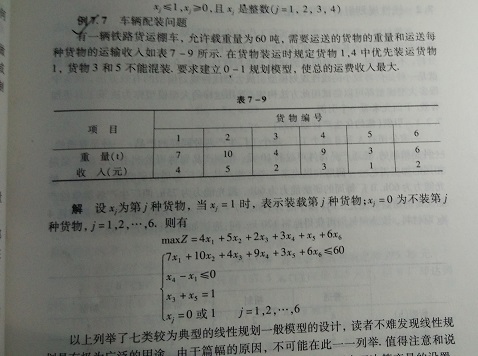
是不是乍一看是“0-1背包”问题呀，我也这么想，于是就这么兴致勃勃的开始用这个想法去思考怎么算。但是算法也忘得差不多，回去赶紧补补，也趁着这次机会好好复习一下算法，于是觉得“0-1背包”问题实现了，这个问题也差不多了吧：

/***********************0-1背包*************************************/

 //先将那两个条件忽略，单纯利用动态规划 -------------------这里就看出有多傻-—_--
 //利用动态规划求解
 #include <iostream>
 #define MAX_NUM 50
 #define MAX_WEIGHT 100
 using namespace std;

 //动态规划求解
 int zero_one_pack(int total_weight, int w[], int v[], int flag[], int n) {
     int c[MAX_NUM + ][MAX_WEIGHT + ] = {  }; //c[i][j]表示前i个物体放入容量为j的背包获得的最大价值
     // c[i][j] = max{c[i-1][j], c[i-1][j-w[i]]+v[i]}
     //第i件物品要么放，要么不放
     //如果第i件物品不放的话,就相当于求前i-1件物体放入容量为j的背包获得的最大价值
     //如果第i件物品放进去的话,就相当于求前i-1件物体放入容量为j-w[i]的背包获得的最大价值
     for (int i = ; i <= n; i++) {
         for (int j = ; j <= total_weight; j++) {
             if (w[i] > j ) {
                 // 说明第i件物品大于背包的重量，放不进去
                 c[i][j] = c[i - ][j];
             }

             else {
                 //说明第i件物品的重量小于背包的重量，所以可以选择第i件物品放还是不放
                 if (c[i - ][j] > v[i] + c[i - ][j - w[i]]) {
                     c[i][j] = c[i - ][j];
                 }
                 else {
                     c[i][j] = v[i] + c[i - ][j - w[i]];
                 }
             }
         }
     }

     //下面求解哪个物品应该放进背包
     int i = n, j = total_weight;
     while (c[i][j] != ) {
         if (c[i - ][j - w[i]] + v[i] == c[i][j]) {
             // 如果第i个物体在背包，那么显然去掉这个物品之后，前面i-1个物体在重量为j-w[i]的背包下价值是最大的
             flag[i] = ;
             j -= w[i];
         }
         --i;
     }
     return c[n][total_weight];
 }

 //回溯法求解

 int main() {
     int total_weight = ;
     int w[] = { ,, , , , , };
     int v[] = { ,, , , ,  ,};
     int flag[]; //flag[i][j]表示在容量为j的时候是否将第i件物品放入背包
     int total_value = zero_one_pack(total_weight, w, v, flag, );
     cout << "需要放入的物品如下" << endl;
     for (int i = ; i <= ; i++) {
         if (flag[i] == )
             cout << i << "重量为" << w[i] << ", 价值为" << v[i] << endl;
     }
     cout << "总的价值为: " << total_value << endl;
     system("pause");
     return ;
 }

查看一下结果，

卧槽，瞎了。背包值这么大原来！于是乎还是想着如何利用“0-1背包”解决，但越想越不对劲，要让程序记住所有路径然后根据条件进行筛选，发现是在太过于复杂。但什么算法可以呢，于是想到了N皇后问题，介于设置的最大载重量太大，不具代表性，于是大大减少最大载重量，设计一下，行表示要存放的对象，列用1，0表示是否要放入，利用不断的回溯递归取得所有可能的值，再选择最大值：

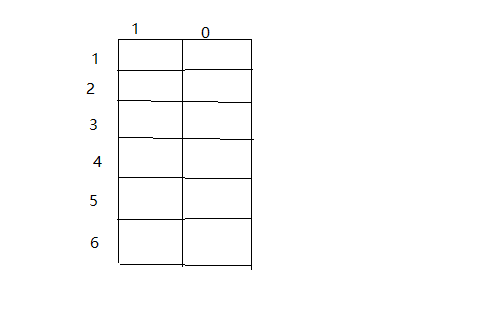
/***********************N皇后*****************************************/

 #include <iostream>
 using namespace std;

 int total_weight = ; //修改最大值
 int w[] = { , , , , , ,  };
 int v[] = { , , , , , ,  };
 int result[] = {  };
 int result_all[][] ;//用于存储所有的可能结果
 int indi = ; //结果指针
 int num = ;

 int sumV();
 int sumW(int n);

 //判断下一个是否符合条件
 bool judge(int n)
 {
     if (n == )
     {
         if (result[] >= result[])
             return true;
         else
             return false;

     }
     if (n == )
     {
         if ((result[] + result[]) == )
             return true;
         else
             return false;
     }

     if (sumW(n) > total_weight)
         return false;
     return true;
 }

 //主要的递归调用函数
 void backtrack(int n)
 {
     if (n > num)

     {

         for (int i = ; i <= num; i++)
         {
             result_all[indi][i] = result[i];
         }
         indi++;
     }

     else
     {
         for (int i = ; i >= ; i--)
         {
             result[n] = i;
             if (judge(n))
                 backtrack(n+);
         }
     }
 }

 //计算综价值
 int sumV(  )
 {
     int m = ;
     for (int i = ; i <= num; i++)
     {
         if (result[i] == )
             m += v[i];
     }
     return m;
 }
 //计算重量
 int sumW(int n)
 {
     int m = ;
     for (int i = ; i <= n; i++)
     {
         if (result[i] == )
             m += w[i];
     }
     return m;
 }

 int main()
 {
     backtrack();

     //计算最大值
     int most = ;
     int pos = ;
     for (int i = ; i < indi; i++)
     {
         int temp = ;
         for (int j = ; j <= num; j++)
         {
             if (result_all[i][j] == )
                 temp += v[j];
         }
         if (temp>most)
         {
             most = temp;
             pos = i;

         }
     }

     cout << "最大值是："<<most<<endl;
     cout << "结果是：" << endl;
     for (int i = ; i <= num; i++)
     {
         cout << result_all[pos][i]<<"   ";
     }
     cout << endl;
     system("pause");
 }

结果：

所以说啊，算法死记硬背是没啥用的，还得看具体情况来，算法还得多学，这次教训大了。