POJ(2784)Buy or Build

Buy or Build

Time Limit: 2000MS		Memory Limit: 65536K
Total Submissions: 1369		Accepted: 542

Description

World Wide Networks (WWN) is a leading company that operates large telecommunication networks. WWN would like to setup a new network in Borduria, a nice country that recently managed to get rid of its military dictator Kurvi-Tasch and which is now seeking for investments of international companies (for a complete description of Borduria, have a look to the following Tintin albums ``King Ottokar's Sceptre", ``The Calculus Affair" and ``Tintin and the Picaros"). You are requested to help WWN todecide how to setup its network for a minimal total cost.
Problem

There are several local companies running small networks (called
subnetworks in the following) that partially cover the n largest cities
of Borduria. WWN would like to setup a network that connects all n
cities. To achieve this, it can either build edges between cities from
scratch or it can buy one or several subnetworks from local companies.
You are requested to help WWN to decide how to setup its network for a
minimal total cost.

• All n cities are located by their two-dimensional Cartesian coordinates.
• There are q existing subnetworks. If q>=1 then each
  subnetwork c ( 1<=c<=q ) is defined by a set of interconnected
  cities (the exact shape of a subnetwork is not relevant to our problem).
• A subnetwork c can be bought for a total cost wc and it cannot be split (i.e., the network cannot be fractioned).
• To connect two cities that are not connected through the
  subnetworks bought, WWN has to build an edge whose cost is exactly the
  square of the Euclidean distance between the cities.

You have to decide which existing networks you buy and which edges
you setup so that the total cost is minimal. Note that the number of
existing networks is always very small (typically smaller than 8).

A 115 Cities Instance

Consider a 115 cities instance of the problem with 4 subnetworks
(the 4 first graphs in Figure 1). As mentioned earlier the exact shape
of a subnetwork is not relevant still, to keep figures easy to read, we
have assumed an arbitrary tree like structure for each subnetworks. The
bottom network in Figure 1 corresponds to the solution in which the
first and the third networks have been bought. Thin edges correspond to
edges build from scratch while thick edges are those from one of the
initial networks.

Input

The
first line contains the number n of cities in the country (
1<=n<=1000 ) followed by the number q of existing subnetworks (
0<=q<=8 ). Cities are identified by a unique integer value ranging
from 1 to n . The first line is followed by q lines (one per
subnetwork), all of them following the same pattern: The first integer
is the number of cities in the subnetwork. The second integer is the the
cost of the subnetwork (not greater than 2 x 10⁶ ). The
remaining integers on the line (as many as the number of cities in the
subnetwork) are the identifiers of the cities in the subnetwork. The
last part of the file contains n lines that provide the coordinates of
the cities (city 1 on the first line, city 2 on the second one, etc).
Each line is made of 2 integer values (ranging from 0 to 3000)
corresponding to the integer coordinates of the city.

Output

Your program has to write the optimal total cost to interconnect all cities.

Sample Input

7 3
2 4 1 2
3 3 3 6 7
3 9 2 4 5
0 2
4 0
2 0
4 2
1 3
0 5
4 4

Sample Output

17

Hint

Sample Explanation: The above instance is shown in Figure 2. An optimal solution is described in Figure 3 (thick edges come from an existing network while thin edges have been setup from scratch).




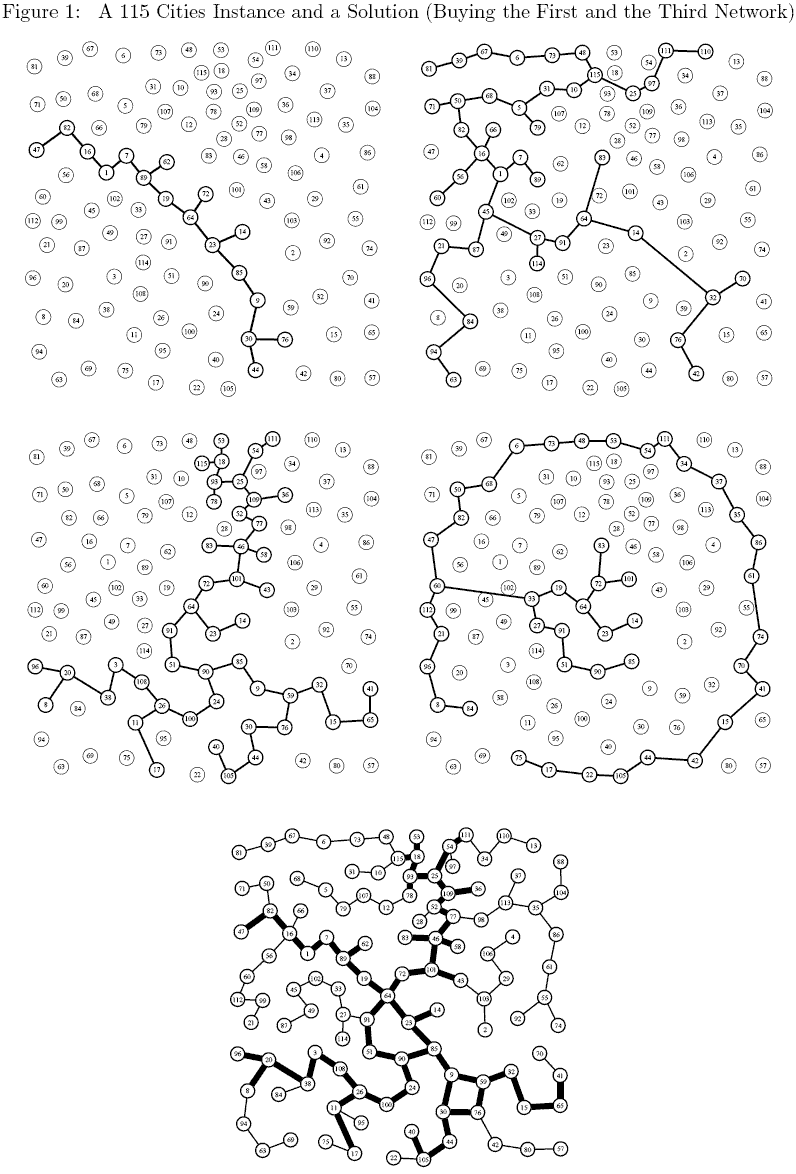
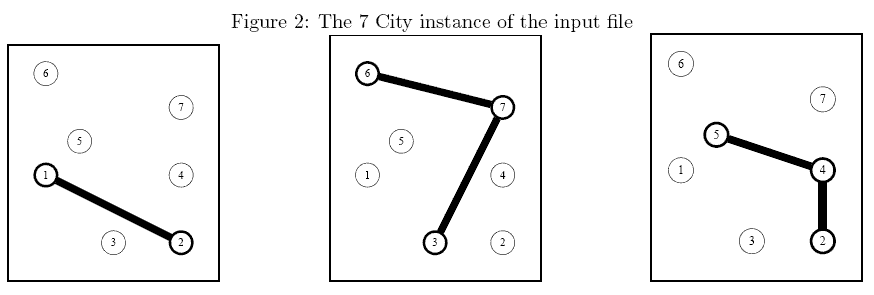
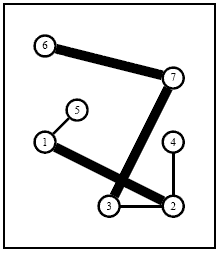
Figure 3: An optimal solution of the 7 City instance in which which
the first and second existing networkshave been bought while two extra
edges (1, 5) and (2, 4)

Source

Southwestern Europe 2005

题意：使n个城市全部连同所需要的最低花费。其中可以购买方案来代替修建。

知识点：图论，最小生成树，状态压缩，枚举。

思路：1.“n个城市”，"连通",“最低花费",可以想到最小生成树。按每条边的权值（权值是一个统称，在这里指的的是距离长短)排序,然后用Kruskal算法得到最小生成树。2.由于方案数q小于8，数字很小考虑到状态压缩，2的q次方种情况一一枚举得到最小值。（PS：在上述1中可以得到所有方案都不购买的情况）。

 #include <iostream>
 #include <cstdio>
 #include <cstring>
 #include <algorithm>
 #include<cmath>
 #include<sstream>
 #include<string>
 using namespace std;
 #define M 10000
 int t,n,m,k,num;
 int root[];
 struct Node
 {
     int x;
     int y;
 };//city corrdinate（城市坐标）
 Node node[];
 struct Buy
 {
     int a[];
     int cost;
     int k;
 };//project（方案）
 Buy buy[];
 int vis[];
 struct Edage
 {
     int u;
     int v;
     int len;
     bool operator<(const Edage &a)const //自定义小于号用于边的排序。
     {
         return len<a.len;
     }
 };
 Edage edage[];
 int cal(int a,int b)
 {
     int dis=(node[a].x-node[b].x)*(node[a].x-node[b].x)+(node[a].y-node[b].y)*(node[a].y-node[b].y);
     return dis;
 }
 void add_edage(int a,int b)
 {
     edage[num].u=a;
     edage[num].v=b;
     edage[num].len=cal(a,b);
     num++;
 }//建边
 void init()
 {
     for(int i=;i<=n;i++)
         root[i]=i;
 }
 int fi(int x)
 {
     int k,j,r;
     r=x;
     while(r!=root[r])
         r=root[r];
     k=x;
     while(k!=r)
     {
         j=root[k];
         root[k]=r;
         k=j;
     }
     return r;
 }
 void uni(int a,int b)
 {
     int x=fi(a);
     int y=fi(b);
     if(x!=y)
     root[x]=y;

 }
 int kruskal()
 {
     int ans=;
     int cnt=;
     for(int i=;i<num;i++)
     {
         int x=fi(edage[i].u);
         int y=fi(edage[i].v);
         if(x!=y)
         {
         root[x]=y;
         ans+=edage[i].len;
         cnt++;}
         if(cnt==n-)
             break;
     }
     return ans;
 }
 void solve()
 {
     init();
     int ans=kruskal();
     //int all=0;
     for(int i=;i<(<<m);i++)//状态压缩
     {
         init();
         int all=;
         for(int j=;j<m;j++)
         {
             if(i&(<<j))//取方案
             continue;
             for(int k=;k<buy[j].k-;k++)
                 uni(buy[j].a[k],buy[j].a[k+]);
          all+=buy[j].cost;
         }
         ans=min(ans,all+kruskal());//保存最小花费
     }
     printf("%d\n",ans);
 }
 int main()
 {
     scanf("%d",&t);
     while(t--)
     {
         num=;
         memset(vis,,sizeof(vis));
         scanf("%d%d",&n,&m);
         for(int i=;i<m;i++)
         {
             scanf("%d%d",&buy[i].k,&buy[i].cost);
             for(int j=;j<buy[i].k;j++)
             scanf("%d",&buy[i].a[j]);
         }
         for(int i=;i<=n;i++)
             scanf("%d%d",&node[i].x,&node[i].y);

         for(int i=;i<=n;i++)
             for(int j=i+;j<=n;j++)
             add_edage(i,j);
             sort(edage,edage+num);
             solve();
         if (t) puts("");

     }

     return ;
 }
 //1
 //
 //7 3
 //2 4 1 2
 //3 3 3 6 7
 //3 9 2 4 5
 //0 2
 //4 0
 //2 0
 //4 2
 //1 3
 //0 5
 //4 4