Python实现二分法和黄金分割法

　　运筹学课上，首先介绍了非线性规划算法中的无约束规划算法。二分法和黄金分割法是属于无约束规划算法的一维搜索法中的代表。

　　二分法:$$x_{1}^{(k+1)}=\frac{1}{2}(x_{R}^{(k)}+x_{L}^{(k)}-\Delta)$$$$x_{2}^{(k+1)}=\frac{1}{2}(x_{R}^{(k)}+x_{L}^{(k)}+\Delta)$$

　　黄金分割法:$$x_{1}^{(k+1)}=x_{R}^{(k)}-(\frac{\sqrt{5}-1}{2})(x_{R}^{(k)}-x_{L}^{(k)})$$$$x_{2}^{(k+1)}=x_{L}^{(k)}+(\frac{\sqrt{5}-1}{2})(x_{R}^{(k)}-x_{L}^{(k)})$$

　　选择的$x_{1}^{(k+1)}$和$x_{2}^{(k+1)}$一定满足$$x_{L}^{(k)}<x_{1}^{(k+1)}<x_{2}^{(k+1)}<x_{R}^{(k)}$$

　　下面确定新的不确定空间$I^{(k+1)}$

　　情况1:若$f(x_{1}^{(k+1)})>f(x_{2}^{(k+1)})$,则$I^{(k+1)}=\left[x_{L}^{(k)},x_{2}^{(k+1)}\right]$

　　情况2:若$f(x_{1}^{(k+1)})<f(x_{2}^{(k+1)})$,则$I^{(k+1)}=\left[x_{1}^{(k+1)},x_{R}^{(k)}\right]$

　　情况3:若$f(x_{1}^{(k+1)})=f(x_{2}^{(k+1)})$,则$I^{(k+1)}=\left[x_{1}^{(k+1)},x_{2}^{(k+1)}\right]$

　　下面记录下用Python实现二分法和黄金分割法的代码。

　　二分法：

 import math
 import numpy as np

 def anyfunction(x):  # 在这里我们定义任意一个指定初始区间内的单峰函数,以x*cos(x)为例
     return x*math.cos(x)

 Low = float(input("Please enter the lowbound: "))
 High = float(input("Please enter the highbound: "))
 High = np.pi  # 在这里我们取初始上界为π,如果可以输入则注释掉这一行
 echos = int(input("Please enter the echos: "))  # 迭代次数
 small = float(input("Please enter the smallvalue: "))  # 公式中的Delta

 for i in range(1, echos + 1):
     Lowvalue = anyfunction(0.5*(Low + High - small))
     Highvalue = anyfunction(0.5*(Low + High + small))
     print("echos: " + str(i))
     print('before ' + "Lowbound: " + str(0.5*(Low + High - small)) + " Highbound: " + str(0.5*(Low + High + small)))
     print('Lowvalue: ' + str(Lowvalue) + ' ' + 'Highvalue: ' + str(Highvalue))
     if(Lowvalue == Highvalue):
         Low = 0.5*(Low + High - small)
         High = 0.5*(Low + High + small)
     elif(Lowvalue < Highvalue):
         Low = 0.5*(Low + High - small)
     else:
         High = 0.5*(Low + High + small)
     print("Lowbound: " + str(Low) + " Highbound: " + str(High))

　　输出结果如下:

　　5次循环后极值点被限制在[0.7828981633974482,0.8907604338221292]内。

　　黄金分割法：

 from math import sqrt, cos
 import numpy as np

 def anyfunction(x):  # 同上以函数x*cos(x)为例
     return x*cos(x)

 Low = float(input("Please enter the lowbound: "))
 High = float(input("Please enter the highbound: "))
 High = np.pi  # 同上，使用时应该注释掉
 echos = int(input("Please enter the echos: "))

 # 初始化，第一次运算不存在运算简化
 uniquevalue = ((sqrt(5)-1)/2)*(High-Low)
 value1 = anyfunction(High - uniquevalue)
 value2 = anyfunction(Low + uniquevalue)

 for i in range(1, echos + 1):
     print("echos: " + str(i))
     print('before ' + "Lowbound: " + str(High - uniquevalue) + " Highbound: " + str(Low + uniquevalue))
     print('value1: ' + str(value1) + ' ' + 'value2: ' + str(value2))
     # 利用黄金分割法的性质减少一半的运算量
     if(value1 == value2):
         Low = High - uniquevalue
         High = Low + uniquevalue
         uniquevalue = ((sqrt(5)-1)/2)*(High-Low)
         value1 = anyfunction(High - uniquevalue)
         value2 = anyfunction(Low + uniquevalue)
     elif(value1 < value2):
         Low = High - uniquevalue
         uniquevalue = ((sqrt(5)-1)/2)*(High-Low)
         value1 = value2
         value2 = anyfunction(Low + uniquevalue)
     else:
         High = Low + uniquevalue
         uniquevalue = ((sqrt(5)-1)/2)*(High-Low)
         value2 = value1
         value1 = anyfunction(High - uniquevalue)
     print("Lowbound: " + str(Low) + " Highbound: " + str(High))

　　输出结果如下: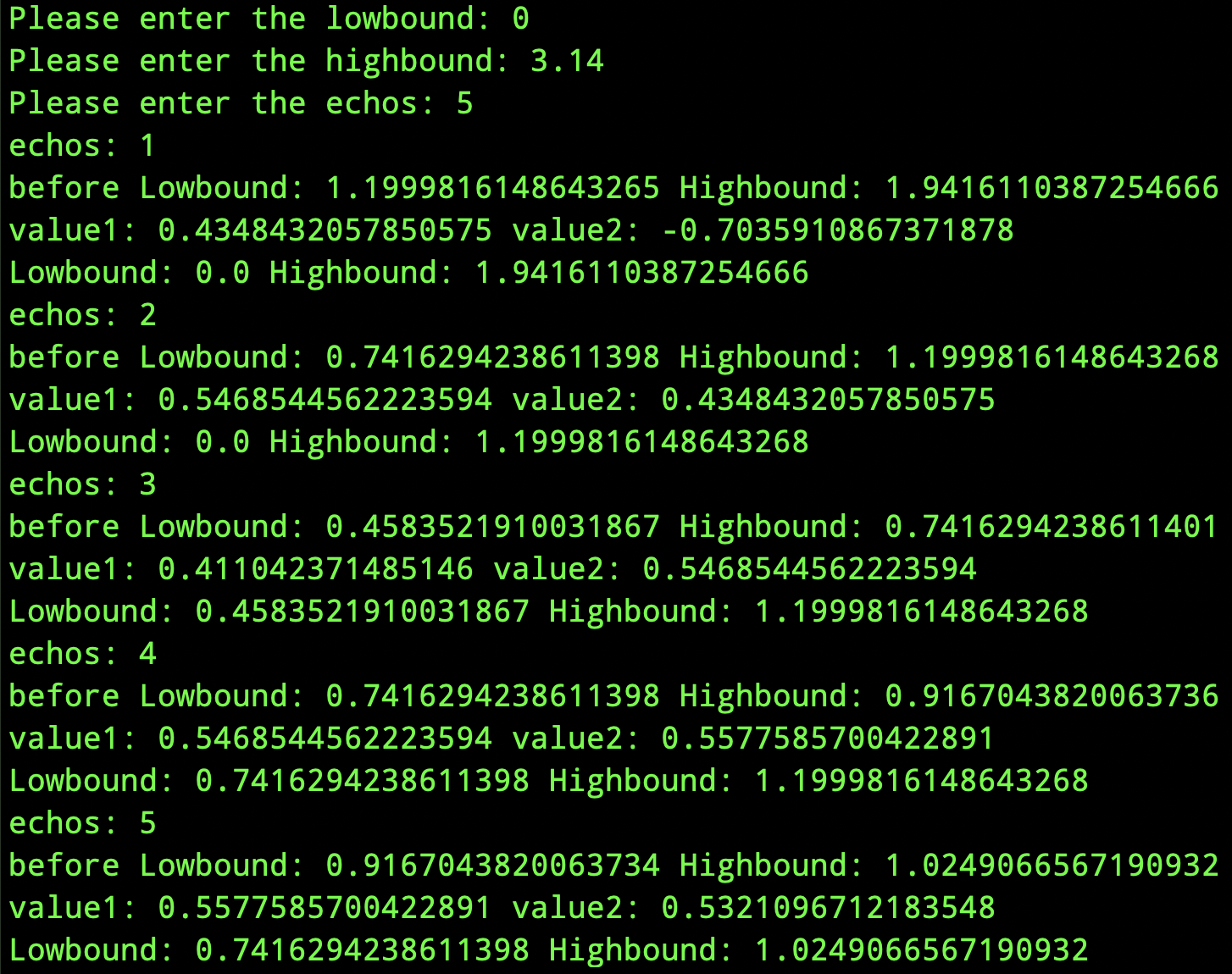

　　5次循环后极值点被限制在[0.7416294238611398,1.0249066567190932]