善意的投票&小M的作物 题解

善意的投票：

因为只有\(2\)种意愿，不妨让想睡午觉的和源点连边，让不想睡午觉的和汇点连边。对于每一对好朋友，在他们之间连边。那么只要源点和汇点还联通，就存在一对好友是冲突的，我们现在要做的就是删去最少的边，使得源点和汇点孤立，问题转化为最小割，用最大流求解即可。

#include <bits/stdc++.h>
int n,m;
int S,T;
int head[200000],tot=1;
int cur[200000];
int deep[200000];
std::queue<int>q;
struct edge{
	int to;
	int nxt;
	int flow;
}e[200000];
void add(int x,int y,int flow){
	e[++tot]={y,head[x],flow};
	head[x]=tot;
	e[++tot]={x,head[y],0};
	head[y]=tot;
}
bool bfs(){
	memset(deep,0,sizeof deep);
	deep[S]=1;
	q.push(S);
	while(!q.empty()){
		int X=q.front();
		q.pop();
		for(int i=head[X];i;i=e[i].nxt){
			int y=e[i].to;
			if(!deep[y]&&e[i].flow){
				deep[y]=deep[X]+1;
				q.push(y);
			}
		}
	}
	return deep[T];
}
int dfs(int x,int flow){
	if(x==T||!flow)
		return flow;
	int Flow=0;
	for(int &i=cur[x];i;i=e[i].nxt){
		int y=e[i].to;
		if(e[i].flow&&deep[y]==deep[x]+1){
			if(int w=dfs(y,std::min(flow,e[i].flow))){
				e[i].flow-=w;
				e[i^1].flow+=w;
				Flow+=w;
				flow-=w;
				if(!flow)
				  break;
			}
		}
	}
	return Flow;
}
void dinic(){
	int maxflow=0;
	while(bfs()){
		memcpy(cur,head,sizeof head);
		while(int w=dfs(S,0x3f3f3f3f))
		  maxflow+=w;
	}
	printf("%d\n",maxflow);
}
main(){
	scanf("%d%d",&n,&m);
	S=n+1;T=S+1;
	for(int i=1,x;i<=n;++i){
		scanf("%d",&x);
		if(x)add(i,T,1);
	  else add(S,i,1);
	}
	for(int i=1,x,y;i<=m;++i){
		scanf("%d%d",&x,&y);
		add(x,y,1);
		add(y,x,1);
	}
	dinic();
	return 0;
}

再考虑小\(M\)的作物，按照之前的做法，对于每种作物，向源点和汇点分别连对应价值流量大小的边，考虑那些组合收益，假设我们需要获得那些作物在\(A\)中的收益，那么当组合中的所有点都和\(B\)断开后，我们才能保留这条边，所以我们可以这样连边：源点到这个点对应的点\(x\)，流量为组合中的作物都种在\(A\)的价值，这个点向所有组合中的点连边，边权都为\(\infty\)。组合中的作物都对这个点对应的点\(x'\)连边，流量为\(\infty\)，\(x'\)向汇点连边，流量为组合都种在\(B\)的价值。



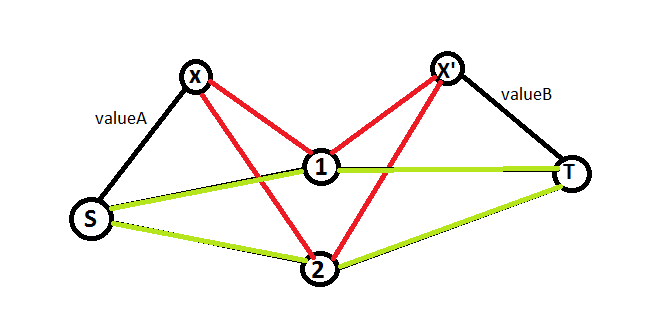
问题得解。

#include <bits/stdc++.h>
#define int long long
int n,kind,S=1,T=2;
int ans;
int head[1000001],tot=1;
int cur[1000000];
int deep[5001];
struct edge{
	int to,nxt,flow;
}e[4000000];
std::queue<int>q;
void add(int x,int y,int flow){
	e[++tot]={y,head[x],flow};
	head[x]=tot;
	e[++tot]={x,head[y],0};
	head[y]=tot;
}
bool bfs(){
	while(!q.empty())q.pop();
	memset(deep,-1,sizeof deep);
	deep[S]=0;
	for(int i=0;i<=tot;++i)
		cur[i]=head[i];
	q.push(S);
	while(!q.empty()){
		int X=q.front();
		q.pop();
		for(int i=head[X],y;i;i=e[i].nxt){
		  y=e[i].to;
		  if(deep[y]<0&&e[i].flow){
		  	deep[y]=deep[X]+1;
		  	q.push(y);
		  	if(y==T)
				  return 1;
		  }
		}
	}
	return 0;
}
int dfs(int x,int flow){
	if(x==T||!flow)
	  return flow;
	int Flow=0;
	for(int &i=cur[x],y;i;i=e[i].nxt){
		y=e[i].to;
		if(e[i].flow&&deep[y]==deep[x]+1){
			if(int w=dfs(y,std::min(flow,e[i].flow))){
				e[i].flow-=w;
				e[i^1].flow+=w;
				Flow+=w;
				flow-=w;
				if(!flow)break;
			}
		}
	}
	if(!flow)
	  deep[x]=-1;
	return Flow;
}
void dinic(){
	while(bfs())
		ans-=dfs(S,1e9);
	printf("%lld\n",ans);
}
main(){
	scanf("%lld",&n);
	for(int i=1,x;i<=n;++i){
		scanf("%lld",&x);
		add(S,i+2,x);
		ans+=x;
	}
	for(int i=1,x;i<=n;++i){
		scanf("%lld",&x);
		add(i+2,T,x);
		ans+=x;
	}
	scanf("%d",&kind);
	for(int i=1,th,valueA,valueB;i<=kind;++i){
		scanf("%lld%lld%lld",&th,&valueA,&valueB);
		ans+=valueA+valueB;
		add(S,n+2+i,valueA);
		add(n+2+i+kind,T,valueB);
		for(int j=1,x;j<=th;++j){
			scanf("%lld",&x);
			add(n+2+i,2+x,1e6);
			add(2+x,n+2+i+kind,1e6);
		}
	}
	dinic();
	return 0;
}