Java 重建二叉树 根据前序中序重建二叉树

题目：输入某二叉树的前序遍历和中序遍历的结果，请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}，则重建二叉树并返回。

解题所需的知识

二叉树的遍历

​ 这个先中后，是根据何时遍历根节点命名的，左的优先级大于后，比如先序就先遍历根结点,再遍历左节点，最后遍历右节点，中序同理，先左中根最后右，后序，先左再右后根。

二叉树的先序遍历

​ 来！ 根据上面的的顺序我们来走一遍，先根再左最后右。

​ 首先，显而意见，1是根节点

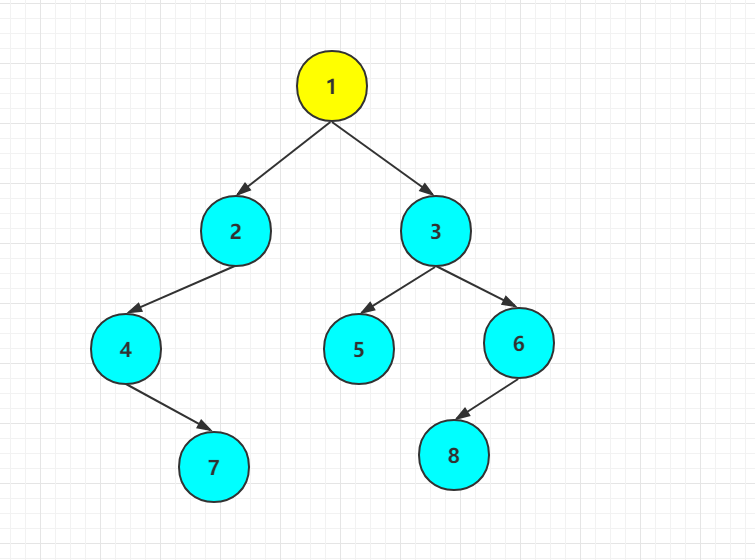
​ 那么现在往左走，发现 2，4，7 也是一棵二叉树，他也是二叉树，我们可不能区别对待，所以理应也满足先序遍历，先根再左最后右。那么2就是这颗小二叉树的根节点啦。

​ 找到了小二叉树的根节点，按照先序再走左，发现4，7也是一棵二叉树，这颗小小二叉树也得满足先序哦，4为根节点，再走左，发现左没了，还记得先序得遍历规则嘛 先根再左后右，左没了那就轮到右啦，所以应该走7了，走完7以后，4，7这棵小小小二叉树算是走完了，走完之后该走2，4，7这颗小二叉树的右节点了，依次类推哦。

先序遍历为 1，2，4，7，3，5，6，8

二叉树的中序遍历

同上 4，7，2，1，5，3，8，6

二叉树的后序遍历

同上 7,4,2,5,8,6,3,1

根据先序，中序构建二叉树

​ 举例 前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}

​ 首先，先序先遍历根节点，那么1显然就是最上面的那个根节点，中序是中间遍历根节点，那么显然可以得出如下图

​ 那么继续去前序得数组中找，发现4，7，2最先出现的是2，那显然2是4，7，2的根结点，去中序找，4，7都在2之前，那显然都是2的左子树。

​ 再去先序找，发现4先出现，那么4就是4，7的根节点，去中序找，发现7在4的右边，说明是右子树。

​ 右子树依次类推。。。。。

代码实现

​ 人用迭代，神用递归

​ 我们用递归的思想，首先先序{1,2,4,7,3,5,6,8}，中序{4,7,2,1,5,3,8,6}，那么我们找到1是根节点：

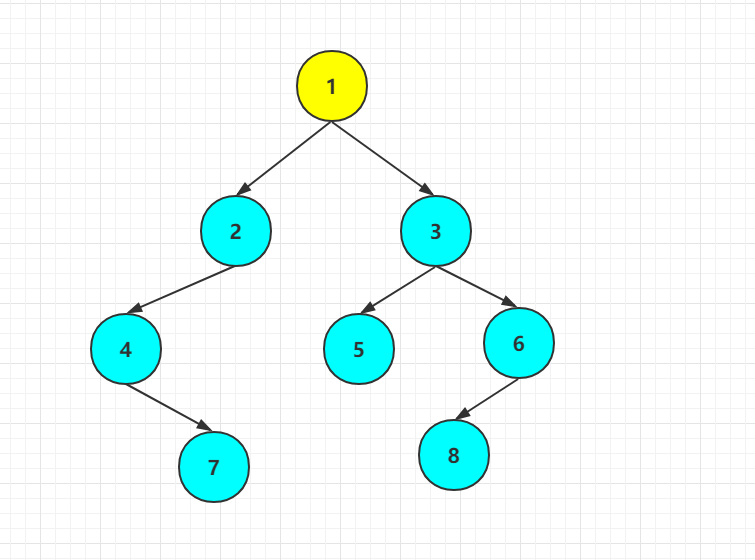
​ 那么现在我们把4，7，2当成一棵二叉树，那么先序从上面知道是{2，4，7} 中序根据上面也知道是{4，7，2}，那接下来跟我们找出1是根节点然后分左右是不是一模一样，只不过先序的数组和中序的数组变了

​

/**
 * Definition for binary tree
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
public class Solution {
   //前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}
    public TreeNode reConstructBinaryTree(int[] pre, int[] in) {

        int len = pre.length;

        TreeNode root = new TreeNode(pre[0]);
        //说明只剩下一个了，表示叶子节点,递归可以退出了
        if (pre.length == 1) {
            root.left = null;
            root.right = null;
            return root;
        }

        //中间值 在{4,7,2,1,5,3,8,6} 这个中间值第一次应该是3
        int flag = 0;
        for (int i = 0; i < len; i++) {
            //在中序中找到
            if (pre[0] == in[i]) {
                flag = i;
                break;
            }
        }
        if (flag > 0) {
            //左子树的先序
            int[] leftPre = new int[flag];
            //左子树的中序
            int[] leftIn = new int[flag];
            for (int j = 0; j < flag; j++) {
                leftPre[j] = pre[j + 1];
            }
            for (int j = 0; j < flag; j++) {
                leftIn[j] = in[j];
            }
            //左子树递归
            root.left = reConstructBinaryTree(leftPre, leftIn);
        } else {
            root.left = null;
        }
        if (pre.length - flag - 1 > 0) {
            //右子树的先序,长度为 总-根-左子树
            int[] rightPre = new int[pre.length - 1 - flag];
            //右子树的中序
            int[] rightIn = new int[pre.length - 1 - flag];

            for (int j = flag + 1; j < len; j++) {
                //右子树中序，为什么要j-flag-1呢 因为我的rightIn要从0开始 而j是k+1开始的 ，所以很尴尬，只能用j-flag-1
                rightIn[j - flag - 1] = in[j];

                rightPre[j - flag - 1] = pre[j];
            }

            root.right = reConstructBinaryTree(rightPre, rightIn);
        } else {
            root.right = null;
        }

        return root;

    }

}