Canvas中绘制贝塞尔曲线

①

什么是贝塞尔曲线？

在数学的数值分析领域中，贝济埃曲线（英语：Bézier curve，亦作“贝塞尔”）是计算机图形学中相当重要的参数曲线。更高维度的广泛化贝济埃曲线就称作贝济埃曲面，其中贝济埃三角是一种特殊的实例。

贝济埃曲线于1962年，由法国工程师皮埃尔·贝济埃（Pierre Bézier）所广泛发表，他运用贝济埃曲线来为汽车的主体进行设计。贝济埃曲线最初由Paul de Casteljau于1959年运用de Casteljau算法开发，以稳定数值的方法求出贝济埃曲线。

Photoshop的钢笔工具 GO！

贝塞尔曲线参考书 GO！

②

原文地址：http://www.cnblogs.com/duanhuajian/archive/2012/10/15/2725096.html

二次贝塞尔曲线

　　quadraticCurveTo(cpx,cpy,x,y)　　//cpx，cpy表示控制点的坐标, x，y表示终点坐标；

数学公式表示如下：

二次方贝兹曲线的路径由给定点P₀、P₁、P₂的函数B（t）追踪：

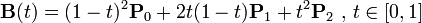
代码实例：

<!DOCTYPE html>

<html>

<head>

<meta charset="utf-8">

<title>canvas直线</title>

<meta name="Keywords" content="">

<meta name="author" content="@my_programmer">

<style type="text/css">

    body, h1{margin:0;}

    canvas{margin: 20px;}

</style>

</head>

<body onload="draw()">

    <h1>二次贝塞尔曲线</h1>

    <canvas id="canvas" width=200 height=200 style="border: 1px solid #ccc;"></canvas>

<script>

    function draw() {

        var canvas=document.getElementById('canvas');

        var context=canvas.getContext('2d');

         //绘制起始点、控制点、终点

          context.beginPath();

          context.moveTo(20,170);

          context.lineTo(130,40);

          context.lineTo(180,150);

          context.stroke();            

          //绘制2次贝塞尔曲线

          context.beginPath();

          context.moveTo(20,170);

          context.quadraticCurveTo(130,40,180,150);

          context.strokeStyle = "red";

          context.stroke();

}

</script>

</body>

</html>

代码效果：

三次贝塞尔曲线

　　bezierCurveTo(cp1x,cp1y,cp2x,cp2y,x,y)　　//cp1x，cp1y表示第一个控制点的坐标, cp2x，cp2y表示第二个控制点的坐标, x，y表示终点的坐标；

数学公式表示如下：

P₀、P₁、P₂、P₃四个点在平面或在三维空间中定义了三次方贝兹曲线。曲线起始于P₀走向P₁，并从P₂的方向来到P₃。一般不会经过P₁或P₂；这两个点只是在那里提供方向资讯。P₀和P₁之间的间距，决定了曲线在转而趋进P₃之前，走向P₂方向的“长度有多长”。

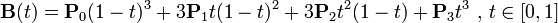
代码实例：

<!DOCTYPE html>

<html>

<head>

<meta charset="utf-8">

<title>canvas直线</title>

<meta name="Keywords" content="">

<meta name="Description" content="">

<style type="text/css">

    body, h1{margin:0;}

    canvas{margin: 20px; }

</style>

</head>

<body onload="draw()">

    <h1>三次贝塞尔曲线</h1>

    <canvas id="canvas" width=200 height=200 style="border: 1px solid #ccc;"></canvas>

<script>

    function draw() {

        var canvas=document.getElementById('canvas');

        var context=canvas.getContext('2d');

       //绘制起始点、控制点、终点

       context.beginPath();

       context.moveTo(25,175);

       context.lineTo(60,80);

       context.lineTo(150,30);

       context.lineTo(170,150);

       context.stroke();  

       //绘制3次贝塞尔曲线

       context.beginPath();

       context.moveTo(25,175);

       context.bezierCurveTo(60,80,150,30,170,150);

       context.strokeStyle = "red";

       context.stroke();

}

</script>

</body>

</html>

代码效果图：

③

原文地址：http://www.cnblogs.com/iamzhanglei/p/6169298.html
HTML5 Canvas玩转酷炫大波浪进度图

如上图所见，本文就是要实现上面那种效果。
由于最近AlloyTouch要写一个下拉刷新的酷炫loading效果。所以首选大波浪进度图。
首先要封装一下大波浪图片进度组件。基本的原理是利用Canvas绘制矢量图和图片素材合成出波浪特效。

本文的代码你可以在这里https://github.com/AlloyTeam/AlloyTouch/blob/master/refresh/wave/image_wave.html找到。

④

二次贝塞尔曲线

<!DOCTYPE html>

<html>

<style type="text/css">

canvas { border: 1px solid black;

width: ;

height: ;

}

</style>

<head>

<meta charset="utf-8">

<title>二次贝塞尔曲线</title>

<link rel="stylesheet" type="text/css">

</head>

<body onload="draw();">

<canvas id="tutorial" width="500" height="500">

</canvas>

<script type="application/javascript">

function draw(){

var canvas = document.getElementById('tutorial');//为 <canvas> 元素得到DOM对象

if (canvas.getContext){ //一旦有了元素对象，你可以通过使用它的getContext() 方法来访问绘画上下文。

var ctx = canvas.getContext('2d'); //这个方法是用来获得渲染上下文和它的绘画功能

//二次贝塞尔曲线

ctx.beginPath();

ctx.moveTo(75,25);

ctx.quadraticCurveTo(25,25,25,62.5);

ctx.quadraticCurveTo(25,100,50,100);

ctx.quadraticCurveTo(50,120,30,125);

ctx.quadraticCurveTo(60,120,65,100);

ctx.quadraticCurveTo(125,100,125,62.5);

cxt.quadraticCurveTo(125,25,75,25);

ctx.stroke();

ctx.closePath();

}

}

</script>

</body>

</html>

渲染对话气泡：

三次贝塞尔曲线

<!DOCTYPE html>

<html>

<style type="text/css">

      canvas { border: 1px solid black;

               width: ;

               height: ;

      }

</style>

<head>

  <meta charset="utf-8">

    <title>三次贝塞尔曲线</title>

  <link rel="stylesheet" type="text/css">

</head>

<body onload="draw();">

  <canvas id="tutorial" width="500" height="500">

  </canvas>

<script type="application/javascript">

  function draw(){

       var canvas = document.getElementById('tutorial');//为 <canvas> 元素得到DOM对象

       if (canvas.getContext){   //一旦有了元素对象，你可以通过使用它的getContext() 方法来访问绘画上下文。

         var ctx = canvas.getContext('2d'); //这个方法是用来获得渲染上下文和它的绘画功能

         //三次贝塞尔曲线

         ctx.beginPath();

         ctx.moveTo(75,40);

         ctx.bezierCurveTo(75,37,70,25,50,25);

         ctx.bezierCurveTo(20,25,20,62.5,20,62.5);

         ctx.bezierCurveTo(20,80,40,102,75,120);

         ctx.bezierCurveTo(110,102,130,80,130,62.5);

         ctx.bezierCurveTo(130,62.5,130,25,100,25);

         ctx.bezierCurveTo(85,25,75,37,75,40);

         ctx.fill();

       }

     }

</script>

</body>

</html>

绘制心形：

Canvas中绘制贝塞尔曲线的更多相关文章

用html5的canvas画布绘制贝塞尔曲线
查看效果:http://keleyi.com/keleyi/phtml/html5/7.htm 完整代码: <!DOCTYPE html PUBLIC "-//W3C//DTD XHT ...
canvas绘制贝塞尔曲线
原文:canvas绘制贝塞尔曲线 1.绘制二次方贝塞尔曲线 quadraticCurveTo(cp1x,cp1y,x,y); 其中参数cp1x和cp1y是控制点的坐标,x和y是终点坐标数学公式表示如 ...
基于canvas二次贝塞尔曲线绘制鲜花
canvas中二次贝塞尔曲线参数说明: cp1x:控制点1横坐标 cp1y:控制点1纵坐标 x: 结束点1横坐标 y:结束点1纵坐标 cp2x:控制点2横坐标 cp2y:控制点2纵坐标 z:结束点2横 ...
NGUI研究院之在Unity中使用贝塞尔曲线（六）[转]
鼎鼎大名的贝塞尔曲线相信大家都耳熟能详.这两天因为工作的原因需要将贝塞尔曲线加在工程中,那么MOMO迅速的研究了一下成果就分享给大家了哦.贝塞尔曲线的原理是由两个点构成的任意角度的曲线,这两个点一个是 ...
Unity3d游戏中自定义贝塞尔曲线编辑器[转]
关于贝塞尔曲线曲线我们再前面的文章提到过<Unity 教程之-在Unity3d中使用贝塞尔曲线>,那么本篇文章我们来深入学习下,并自定义实现贝塞尔曲线编辑器,贝塞尔曲线是最基本的曲线,一般 ...
在Unity中使用贝塞尔曲线(转)
鼎鼎大名的贝塞尔曲线相信大家都耳熟能详.这两天因为工作的原因需要将贝塞尔曲线加在工程中,那么MOMO迅速的研究了一下成果就分享给大家了哦.贝塞尔曲线的原理是由两个点构成的任意角度的曲线,这两个点一个是 ...
NGUI研究之在Unity中使用贝塞尔曲线
鼎鼎大名的贝塞尔曲线相信大家都耳熟能详.这两天由于工作的原因须要将贝塞尔曲线加在project中.那么我迅速的研究了一下成果就分享给大家了哦.贝塞尔曲线的原理是由两个点构成的随意角度的曲线,这两个点一 ...
【Unity3d游戏开发】游戏中的贝塞尔曲线以及其在Unity中的实现
RT,马三最近在参与一款足球游戏的开发,其中涉及到足球的各种运动轨迹和路径,比如射门的轨迹,高吊球,香蕉球的轨迹.最早的版本中马三是使用物理引擎加力的方式实现的足球各种运动,后来的版本中使用了根据物理 ...
HTML5在canvas中绘制复杂形状附效果截图
HTML5在canvas中绘制复杂形状附效果截图一.绘制复杂形状或路径在简单的矩形不能满足需求的情况下,绘图环境提供了如下方法来绘制复杂的形状或路径. beginPath() : 开始绘制一个新路 ...

随机推荐

oracle,mysql,sql server三大数据库的事务隔离级别查看方法
1:mysql的事务隔离级别查看方法 mysql 最简单,执行这条语句就行:select @@tx_isolation 详情: 1.查看当前会话隔离级别 select @@tx_isolation; ...
jsp参数乱码解决
iframe src引入jsp,?跟着的中文参数会乱码解决方法: var CJJG=encodeURI(encodeURI(value.data.CJJG));//js里面转码一次 //jsp页面里 ...
jmeter生成html格式接口自动化测试报告
jmeter生成html格式接口自动化测试报告 jmeter自带执行结果查看的插件,但是需要在jmeter工具中才能查看,如果要向领导提交测试结果,不够方便直观. 笔者刚做了这方面的尝试,总结出来分享 ...
第十五章：Oracle12c 数据库警告日志
一:查看警告日志文件的位置 Oracle 12c环境下查询,alert日志并不在bdump目录下,看到网上和书上都写着可以通过初始化参数background_dump_dest来查看alter日志路径 ...
Scyther
1.Security Protocol :a domain analysis 一个安全协议描述了很多的行为,每一个行为称为角色,例如触发角色和接受角色,一个系统有多个通信代理组成,每一个代理扮演 ...
CSRF & CORS 的区别
转发 CSRF & CORS 的区别下面转的两篇文章分别说明了以下两个概念和一些解决方法: 1. CSRF - Cross-Site Request Forgery - 跨站请求伪造 2. ...
Mybatis自定义分布式二级缓存实现与遇到的一些问题解决方案!
先说两句: 我们都知道Mybatis缓存分两类: 一级缓存(同一个Session会话内) & 二级缓存(基于HashMap实现的以 namespace为范围的缓存) 今天呢, 我们不谈一级缓存 ...
JAVA -数据类型与表达式---变量与赋值
变量程序中所管理的大部分信息,都是用变量表示的.下面讨论如何在程序中声明和使用变量. 变量(variable)代表保存数据的内存单元,变量名是内存单元的符号地址.变量声明要求编译器分配足够大的内存单 ...
oracle ORA-00119, ORA-00132问题解决
使用PL/SQL登录oracle报ORA-12154: TNS: 无法解析指定的连接标识符sqlplus /nologconnect /as sysdbastartup报如下错误:ORA-00119: ...
java思维导图
https://www.edrawsoft.cn/viewer/public/s/eeca7704686971

Canvas中绘制贝塞尔曲线

二次贝塞尔曲线

Canvas中绘制贝塞尔曲线的更多相关文章

随机推荐

热门专题