#10038.A Horrible Poem

#10038.A Horrible Poem

题目传送门

思路解析

既然这道题目在hash板块里，那么自然就可以想到用hash做这道题目。

首先我们可以用hash数组存储字符串的前缀的hash值。

因为我们需要找到S[a..b] 的最短循环节长度，所以我们可以枚举循环节长度 i 。

由于循环要遍历完整个字串。所以设字串长度为 \(len\) ，就有：

if(len%i)continue;

即i为\(len\)的因数。

关于判断循环节，我们最先想到的就是将一个长度为i字串不断往后对比，直到遍历完长度为\(len\)的字串。

如果此时还是没有出现不匹配的情况，那么就可以输出答案i了。

while(Q--){
		int a=read(),b=read(),len=b-a+1;
		for(int i=1;i<=len;++i){
			if(len%i)continue;
			bool flag=1;ull cmp=f[a+i-1]-f[a-1]*p[i];
			for(int j=a+i*2-1;j<=b;j+=i)
				if(f[j]-f[j-i]*p[i]!=cmp){flag=0;break;}
			if(flag){write(i);putchar('\n');break;}
		}
	}

但是这样的做法复杂度为\(O(qn \sqrt n )\) ，显然会超时。(废话)

仔细一想可以发现我们在判断循环节的时候我们浪费了一部分时间，那有没有更快的判断循环节的方法呢？

（显然是有的）

if(H(a,b-i)==H(a+i,b)){write(i);putchar('\n');break;}

这是H函数，表示l~r间的值。

ull H(int l,int r){return f[r]-f[l-1]*p[r-l+1];}

这种做法(当然不是作者独立想出来的啦！)可以将判断循环节的复杂度降到\(O(1)\)。

让我们来理解一下这种做法:

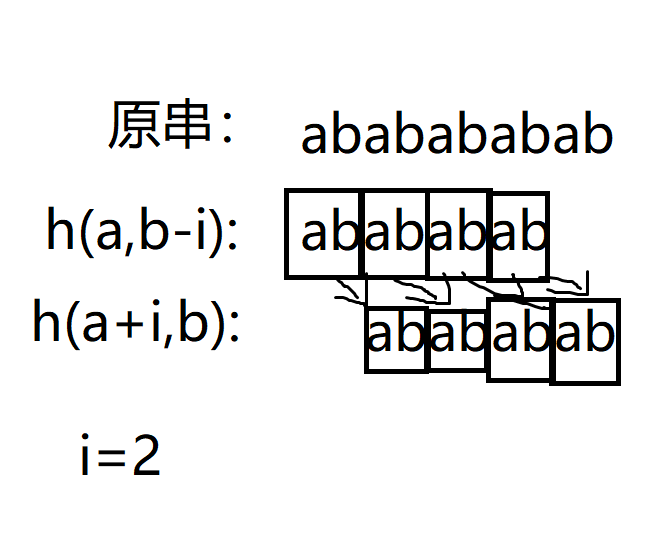
前一个串中的每一个单位都和后面应该单位比较，一但出现有一个不相等就会判为不循环。

于是代码就变成这样：

while(Q--){
		int a=read(),b=read(),len=b-a+1;
		for(int i=1;i<=len;++i){
			if(len%i)continue;
			if(H(a,b-i)==H(a+i,b)){write(i);putchar('\n');break;}
		}
	}

（哈哈哈变短了！）

这样复杂度还是\(O(qn)\)会超时。

这时我们想我们枚举了许多不必要的i，所以只需要把一些不必要的i去掉就可以了。

上代码

#include<bits/stdc++.h>
using namespace std;
typedef unsigned long long ull;
const int N=500005,base=53;
int read(){
    int x=0;char c=getchar();
    while(c<'0'||c>'9')c=getchar();
    while(c>='0'&&c<='9')x=x*10+c-'0',c=getchar();
    return x;
}
char get(){
    char c=getchar();
    while(c<'a'||c>'z')c=getchar();
    return c;
}
void write(int x){if(x/10)write(x/10);putchar(x%10+'0');}
ull f[N],p[N];
int n,ss[N],nxt[N],tmp[N],next[N],tot;
bool vis[N];
char a[N];
ull H(int l,int r){return f[r]-f[l-1]*p[r-l+1];}
int main(){
    p[0]=1;for(int i=1;i<=N;++i)p[i]=p[i-1]*base;
    n=read();f[0]=1;
    for(int i=1;i<=n;++i){
        char ch=get();
        f[i]=f[i-1]*base+ch;
    }
    for(int i=2;i<=n;++i){//欧拉筛
        if(!vis[i]){ss[++tot]=i;next[i]=i;}
        for(int j=1;j<=tot&&(ull)ss[j]*i<=n;++j){
            vis[ss[j]*i]=1;
            next[ss[j]*i]=ss[j];//找出最小的质因数
            if(i%ss[j]==0)break;
        }
    }
    int Q=read();
    while(Q--){
        int a=read(),b=read(),len=b-a+1,sum=0;
        while(len!=1){
            tmp[++sum]=next[len];//tmp数组储存len的所有质因数
            len/=next[len];//此时next数组就可以做到检索出len的所有质因数
        }
        len=b-a+1;
        for(int j=1;j<=sum;++j){
            int k=len/tmp[j];
            //判断长度为k的字串是否能在长度为len的循环中构成循环(一开始原串len视为长度为len的循环)
            //因为在len中可以构成循环就代表着可以在a~b中构成循环
            if(H(a,b-k)==H(a+k,b))len=k;//当字串k构成循环时就可以在字串k中寻找循环节
        }
        write(len);putchar('\n');
    }
    return 0;
}