子数组最小值的总和 Sum of Subarray Minimums

2018-09-27 23:33:49

问题描述：

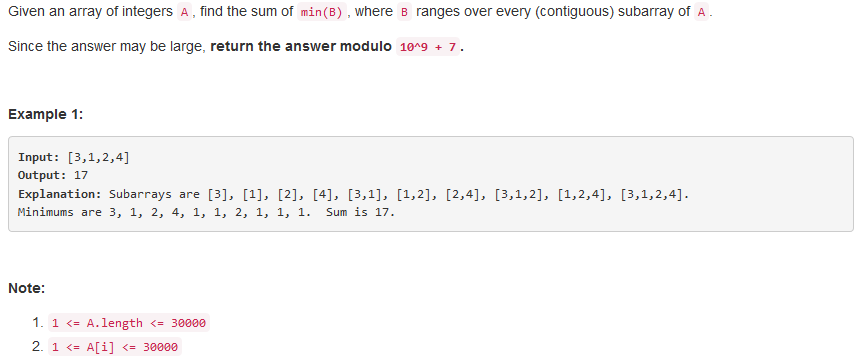
问题求解：

方法一、DP(MLE)

动态规划的想法应该是比较容易想到的解法了，因为非常的直观，但是本题的数据规模还是比较大的，如果直接使用动态规划，即使不MLE，也是肯定会在大规模的数据量上TLE的。

    public int sumSubarrayMins(int[] A) {
        int res = 0;
        int mod = (int)Math.pow(10, 9) + 7;
        int[][] dp = new int[A.length][A.length];
        for (int i = 0; i < A.length; i++) dp[i][i] = A[i];
        for (int len = 2; len <= A.length; len++) {
            for (int i = 0; i <= A.length - len; i++) {
                int j = i + len - 1;
                dp[i][j] = Math.min(dp[i + 1][j], dp[i][j - 1]);
            }
        }
        for (int i = 0; i < A.length; i++) {
            for (int j = 0; j < A.length; j++) {
                res = (res + dp[i][j]) % mod;
            }
        }
        return res;
    }

方法二、

数据量已经基本表明时间复杂度在O(nlogn)左右比较好，那么直接使用dp肯定是不会通过所有的例子的。

本题还有另外一种思路：

res = sum(A[i] * f(i))
where f(i) is the number of subarrays,
in which A[i] is the minimum.

难点就在于求f(i)，为了求f(i)需要求left[i]和right[i]。

left[i]：A[i]左边严格大于A[i]的个数

right[i]：A[i]右边大于等于A[i]的个数

f(i) = (left[i] + 1) * (right[i] + 1)，其实就是一个排列组合，左边取一个可能，那么可以从右边取right[i] + 1种来进行组合。

这里需要特别注意的一点是：首先本问题是允许重复的子数组的，这里的重复是指数字上相等，但是是不允许完全一致的区间，因此左边必须是严格大于，否则会出现重复的情况。计算left，right数组可以使用Stack在O(n)时间复杂度完成求解，最后的res计算也是线性时间，因此总的时间复杂度为O(n)。

    public int sumSubarrayMins(int[] A) {
        int res = 0;
        int mod = (int)1e9 + 7;
        int[] left = new int[A.length];
        int[] right = new int[A.length];
        Stack<int[]> stack = new Stack<>();
        stack.push(new int[]{Integer.MIN_VALUE, -1});
        for (int i = 0; i < A.length; i++) {
            while (stack.peek()[0] > A[i])
                stack.pop();
            left[i] = i - stack.peek()[1];
            stack.push(new int[]{A[i], i});
        }
        stack.clear();
        stack.push(new int[]{Integer.MIN_VALUE, A.length});
        for (int i = A.length - 1; i >= 0; i--) {
            while (stack.peek()[0] >= A[i])
                stack.pop();
            right[i] = stack.peek()[1] - i;
            stack.push(new int[]{A[i], i});
        }
        for (int i = 0; i < A.length; i++) {
            res = (res + A[i] * left[i] * right[i]) % mod;
        }
        return res;
    }