KMP算法（next数组方法）

KMP算法之前需要说一点串的问题：

串：

字符串：ASCII码为基本数据形成的一堆线性结构。

串是一个线性结构；它的存储形式：

typedef struct STRING {

　　CHARACTER *head;

　　int length;

};

朴素的串匹配算法：

设文本串text = "ababcabcacbab",模式串为patten = "abcac"     其匹配过程如下图所示。

黑色线条代表匹配位置，红色斜杠代表失配位置

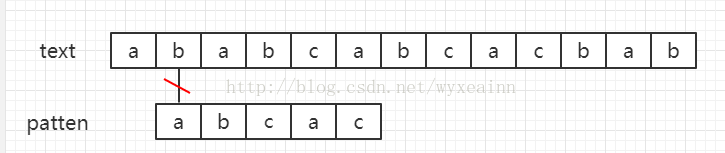
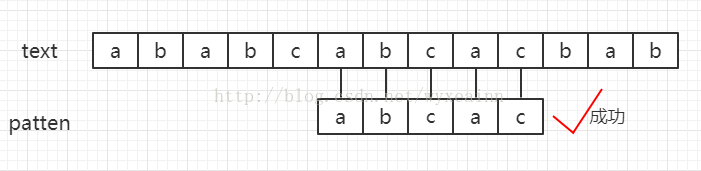
算法说明：

一般匹配字符串时，我们从目标字符串text（假设长度为n）的第一个下标选取和patten长度（长度为m）一样的子字符串进行比较，如果一样，就返回开始处的下标值，不一样，选取text下一个下标，同样选取长度为n的字符串进行比较，直到str的末尾（实际比较时，下标移动到n-m）。在普通的匹配中，假如从文本串的第i个字符来开始于模式串匹配。当匹配到模式串的第j位发现失配，即text[i+j] != patten[j]的时候，我们又从文本串的第i+1个位置来重新开始匹配。尽管我们已经知道了好多字符其实根本就匹配不上，我们还是进行了这个过程，这个时候回溯的过程会非常耗费我们的时间。这样的时间复杂度是O(n*m)。

代码如下：

int search(const char*str,const char *subStr) {
    int strlen = strlen(str);
    int subStrlen = strlen(subStr);
    int i;
    int j;
    for(i = ;i <= strlen - subStrlen;i++){
        for(j = ;j < subStrlen;j++){
            if(str[i + j] != subStr[j])
            break;
        }判断subStrlen是否比较完成
    }
}

KMP算法：

而KMP算法的实质就是，当遇到text[i+j] != patten[j]的时候，但是我们知道模式串中的 0~j-1 位置上的字符已经于i ~ i+j-1位置上的字符是完全匹配的。就不再重新从text[i+1]开始匹配，而是根据next数组的下标找到patten的下标，从那个下标开始匹配。从而时间复杂度为O(m+n)。

例如模式串Patten = "abaabcac"。其next数组如图所示：

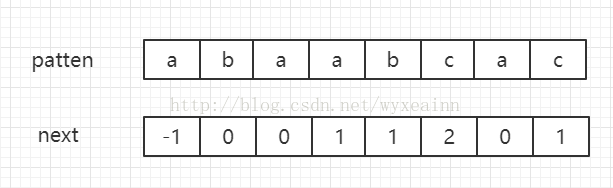
我们可以看到这次的匹配在蓝色的c失配了，而c的下标为5，他的next数组的下标为2。因此，下次的匹配不再是从text[1]开始，而是从text[2]开始，这样就省去了不必要的比较。

代码如下：

#include <stdio.h>
#include <malloc.h>
#include <string.h>

#include "kmpmec.h"

void getNext(const char *str, int *next);
int KMPSearch(const char *str, const char *subStr);

int KMPSearch(const char *str, const char *subStr) {
    int strLen = strlen(str);
    int subLen = strlen(subStr);
    int *next;
    int i = ;
    int j = ;

    if (strLen <=  || subLen <=  || strLen < subLen) {
        return -;
    }
    next = (int *) calloc(sizeof(int), subLen);
    if (subLen > ) {
        getNext(subStr, next);
    }

    while (strLen - i + next[j] >= subLen) {
        while (subStr[j] !=  && str[i] == subStr[j]) {
            i++;
            j++;
        }
        if (subStr[j] == ) {
            free(next);
            return i - subLen;
        } else if (j == ) {
            i++;
            j = ;
        } else {
            j = next[j];
        }
    }

    free(next);
    return -;
}

void getNext(const char *str, int *next) {  //得到next数组
    int i = ;
    int j = ;
    boolean flag;

    next[] = next[] = ;  //next数组的前两个下标一定为零
    for (i = ; str[i]; i++) {
        for (flag = TRUE; flag;) {
            if (str[i-] == str[j]) { //通过比较失配位置的前一个和前一个下标元素的比较，获取next数组的下标。
                next[i] = ++j;
                flag = FALSE;
            } else if (j == ) {
                next[i] = ;
                flag = FALSE;
            } else {
                j = next[j];
            }
        }
    }
}

int main(void) {
    char str[];
    char subStr[];
    int result;

    printf("请输入源字符串:");
    gets(str);
    printf("请输入子字符串:");
    gets(subStr);

    result = KMPSearch(str, subStr);
    if (result == -) {
        printf("字符串[%s]不存在子串[%s]\n", str, subStr);
    } else {
        printf("子串[%s]第一次出现在字符串[%s]中的下标为%d\n", subStr, str, result);
    }

    return ;
}；