acm数论之旅--数论四大定理

ACM数论之旅5---数论四大定理（你怕不怕(☆ﾟ∀ﾟ)老实告诉我）

 

（本篇无证明，想要证明的去找度娘）o(*≧▽≦)ツ

----------数论四大定理---------

数论四大定理：

1.威尔逊定理

2.欧拉定理

3.孙子定理（中国剩余定理）

4.费马小定理

（提示：以后出现（mod p）就表示这个公式是在求余p的条件下成立）

1.威尔逊定理：（PS：威尔逊是个厉害人）

当且仅当p为素数时：( p -1 )! ≡ -1 ( mod p )

或者这么写( p -1 )! ≡ p-1 ( mod p )

或者说

若p为质数，则p能被(p-1)!+1整除

在初等数论中

这是威尔逊给出了判定一个自然数是否为 素数 的 充分必要条件

但是由于阶乘是呈爆炸增长的，其结论对于实际操作意义不大。(´・ω・`)（威尔逊表示很伤心）

2.欧拉定理：（PS：欧拉是个厉害人）

欧拉定理，也称费马-欧拉定理

若n,a为正整数，且n,a互质，即gcd(a,n) = 1，则

a^φ(n) ≡ 1 (mod n)

 

φ(n) 是欧拉函数

  欧拉函数是求小于n的数中与n互质的数的数目  

(o>▽<)太长看不懂？我来帮你断句

  欧拉函数是求 （小于n的数 ）中 （与n互质的数 ）的数目

或者说

  欧拉函数是求 1到n-1 中 与n互质的数 的数目

 

如果n是质数

那么1到n-1所有数都是与n互质的，

所以φ(n) = n-1

如果n是合数。。。自己算吧

例如φ(8)=4，因为1,3,5,7均和8互质

 

 

顺便一提，这是欧拉定理

φ(n)是欧拉函数

还有一个欧拉公式

e^ix = cosx + isinx

把x用π带进去，变成

e^iπ= -1

大部分人写成 e^iπ + 1 = 0

 

这是一个令万人膜拜的伟大公式

引用一个名人的话（我忘了是谁(￣▽￣lll)）：

"它把自然对数e，虚数i，无理数π，自然界中的有和无（1和0）巧妙的结合了起来，上帝如果不存在，怎么会有这么优美的公式。

如何见到它第一眼的人没有看到它的魅力，那它一定成不了数学家"

 

一定要分清 欧拉定理，欧拉函数和欧拉公式这3个东西，要不然你就百度不到你想要的东西了（其实我在说我自己￣ε ￣）

 

 

 

 

 

 

 

 

 

 

 

3.孙子定理（中国剩余定理）：（PS：孙子是个厉害人。。。这话怎么在哪里听过( ・◇・)？好耳熟）

孙子定理，又称中国剩余定理。

公元前后的《孙子算经》中有“物不知数”问题：“今有物不知其数，三三数之余二 ，五五数之余三 ，七七数之余二，问物几何？”答为“23”。

就是说，有一个东西不知道有多少个，但是它求余3等于2，求余5等于3，求余7等于2，问这个东西有多少个？”答为“23”。

用现代数学的语言来说明的话，中国剩余定理给出了以下的一元线性同余方程组：

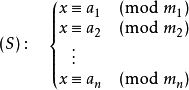
中国剩余定理说明：假设整数m1,m2, ... ,mn两两互质，则对任意的整数：a1,a2, ... ,an，方程组 (S)有解

至于怎么求解，以后再讲

4.费马小定理：（PS：费马是个厉害人。。。好了最后一遍，不玩了）

假如p是质数，若p不能整除a，则 a^(p-1) ≡1（mod p），若p能整除a，则a^(p-1) ≡0（mod p）。

或者说，若p是质数，且a,p互质，那么 a的(p-1)次方除以p的余数恒等于1。

 

 

你看你看你看o(*≧▽≦)ツ，是不是和欧拉定理很像

 

因为欧拉定理是费马小定理的推广，所以欧拉定理也叫费马-欧拉定理（费马：欧拉是坏人（/TДT)/，盗取我的成果，然后加以利用）

顺便一提，费马大定理

费马大定理，又被称为“费马最后的定理”，由法国数学家费马提出。

它断言当整数n >2时，关于x, y, z的方程 x^n + y^n = z^n 没有正整数解。

被提出后，经历多人猜想辩证，历经三百多年的历史，最终在1995年被英国数学家安德鲁·怀尔斯证明。