JS(JavaScript）的深入了解1（更新中···）

面向对象

1.单列模式

2.工厂模式

3.构造函数

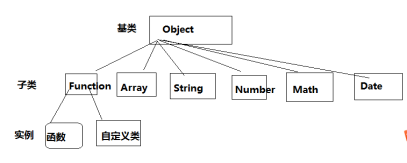
(1) 类Js天生自带的类Object

基类Function Array Number Math Boolean Date Regexp String

1.事件

浏览器客户端上客户触发的行为都称为事件

所有的事件都是天生自带的，不需要我们去绑定，只需要我们去触发。

通过obj.事件名=function(){}

事件名:onmouseover onmouseout onmousedown onmousemove onmouseup

Onclick  onchange onfocus onblur 等等

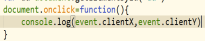
当用户触发一个事件时，浏览器的所有详细信息都存在一个叫event的对象上。

我们把他叫事件对象

所有事件在绑定方法的时候，天生自带一个参数就叫event。

鼠标的坐标

event.clientX

event.ClientY

Event 的兼容性

在chrome下 event是undefined 在Ie低版本下是null，火狐下会报错

document.onclick=function(e){

var e=e||window.event

}

2.事件冒泡

什么叫事件冒泡

当给父子元素的同一事件绑定方法时，触发了子元素身上的事件，执行完毕之后，

也会触发父级元素的相同事件，这种传播机制叫事件冒泡。

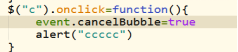
取消事件冒泡

Event对象有个属性叫cancelBubble默认值是false 改成true就取消当前事件冒泡

3.事件捕获

给一个元素绑定事件，普通写法是

obj.onclick=function(){} 这就相当于给obj的onclick属性赋值是一个道理。

obj.onclick=function(){}

这种写法有一点不好，后者会将前者覆盖掉。

事件绑定的第二种写法

标准浏览器用 addEventListener()这个方法

Ie低版本用attachEvent()这个方法

addEventListener(参数1，参数2，参数3)

参数1 是事件名 事件名不能带on

参数2 事件函数

参数3 布尔值，代表捕获不捕获 默认是false 不捕获但是冒泡。

事件捕获

1. ie低版本没有捕获
2. 普通事件绑定写法没有捕获

事件捕获

给父子元素用addEventListener()绑定同一个事件时，当触发子元素身上的事件，会先触发父元

素，然后在传递给子元素，这种传播机制叫事件捕获。

attachEvent()和addEventListener()二者区别

1. attachEvent只用在iE8以下，addEventListener()适合标准浏览器
2. attachEvent的事件名带on 而addEventListener事件名不带on
3. attachEvent函数里面的this是window，而addEventListener函数里面的this是当前元素对象

attachEvent只有冒泡没有捕获addEventListener有冒泡也有捕获

4.Call()和apply()

Call和apply，就是改变函数里面的this指向的方法。

xxx.call()或xxx.apply()

特别强调下xxx必须是function，（普通函数，类，构造函数）

var obj={

name:"志伟"

}

function fn(){

console.log(this.name)

}

fn.call(obj)

Call()中第一个参数是null的时候，函数里的this还是指向原来的，不变。

所有事件都是异步的。