广度优先搜索BFS---求出矩阵中“块”的个数

题目：

　　给出一个 m x n 的矩阵，矩阵中的元素为0或1。如果矩阵中有若干个 1是相邻的，那么称这些1构成了一个“块”。求给定的矩阵中“块”的个数。

0 1 1 1 0 0 1

0 0 1 0 0 0 0

0 0 0 0 1 0 0

0 0 0 1 1 1 0

1 1 1 0 1 0 0

1 1 1 1 0 0 0

例如上面的 6 x 7的矩阵中，“块”的个数为4。

输入格式：

第一行给出 m，n（1<=m，n<= 20）分别表示矩阵的行，列。

每一行给出 n个数（0或者1），共m行。

输出格式：

输出矩阵中“块”的个数。

输入样例：

6 7

0 1 1 1 0 0 1

0 0 1 0 0 0 0

0 0 0 0 1 0 0

0 0 0 1 1 1 0

1 1 1 0 1 0 0

1 1 1 1 0 0 0

输出样例：

4

直接上代码。。。

 #include<iostream>
 #include<queue>
 #include<unordered_map>
 using namespace std;

 const int maxn = ;
 struct Node {
     int x,y;
 } node;//全局的临时变量
 int matrix[maxn][maxn];
 int m,n,CNT = ;
 int X[] = {,,,-};//控制访问的四个方向,新技能 get !!!
 int Y[] = {,-,,};
 bool inque[maxn][maxn] = {false};//标记元素是否已经入队---这样不会改变矩阵原本的状态，新技能get !!!
 bool judge(int i,int j) {
     if(i <  || j <  || i>= m||j>= n || matrix[i][j] ==  || inque[i][j] == true)
         return false;
     return true;
 }
 void BFS(int i, int j) {
     queue<Node> que;                     //定义队列
     node.x = i,node.y = j;
     que.push(node);                      //入队
     inque[i][j] = true;                  //标记已经入队
     while(!que.empty()) {                //队列非空
         Node top = que.front();          //取出队首元素
         que.pop();                       //队首元素出队
         for(int i = ; i < ; ++i) {     //访问相邻的四个元素
             int nowI = top.x + X[i];
             int nowJ = top.y + Y[i];
             if(judge(nowI,nowJ)) {
                 node.x = nowI,node.y = nowJ;
                 que.push(node);          //入队
                 inque[nowI][nowJ] = true;//标记已经入队
             }
         }
     }
 }

 int main() {
     cin>>m>>n;
     for(int i = ; i < m; ++i) { //初始化矩阵
         for(int j = ; j < n; ++j)
             cin>>matrix[i][j];
     }
     for(int i = ; i < m; ++i) {//暴力DFS，哈哈哈
         for(int j = ; j < n; ++j) {
             if(matrix[i][j] ==  && inque[i][j] == false) { //元素为1，并且元素未入过队
                 BFS(i,j);
                 CNT++;
             }
         }
     }
     cout<<CNT;//输出矩阵中”块“ 的个数
     return ;
 }

运行结果：

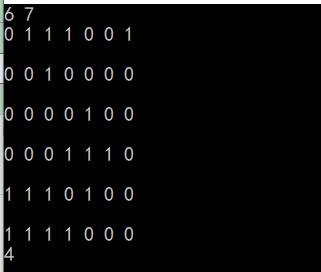
get了两个新技能：

一，设置两个方向数组X,Y来控制4个或者8个方向

二，设置一个全局二维数组，标记元素是否已经入队（而不是访问，因为已经入队的元素，可能还未访问，这是两者的区别），这样可以不改变初始矩阵的状态

总的来说，因为BFS需要队列支持，所以目前我感觉比较难，不过！还好BFS有模版！！！

先要记住大体流程，然后反复练习！！！