python多项式拟合：np.polyfit 和 np.polyld

python数据拟合主要可采用numpy库，库的安装可直接用pip install numpy等。

1. 原始数据：假如要拟合的数据yyy来自sin函数，np.sin

import numpy as np
import matplotlib.pyplot as plt
xxx = np.arange(0, 1000)  # x值，此时表示弧度
yyy = np.sin(xxx*np.pi/180)  #函数值，转化成度

2. 测试不同阶的多项式，例如7阶多项式拟合，使用np.polyfit拟合，np.polyld得到多项式系数

z1 = np.polyfit(xxx, yyy, 7) # 用7次多项式拟合，可改变多项式阶数；
p1 = np.poly1d(z1) #得到多项式系数，按照阶数从高到低排列
print(p1)  #显示多项式

3. 求对应xxx的各项拟合函数值

yvals=p1(xxx) # 可直接使用yvals=np.polyval(z1,xxx)

4. 绘图如下

plt.plot(xxx, yyy, '*',label='original values')
plt.plot(xxx, yvals, 'r',label='polyfit values')
plt.xlabel('x axis')
plt.ylabel('y axis')
plt.legend(loc=4) # 指定legend在图中的位置，类似象限的位置
plt.title('polyfitting')
plt.show()

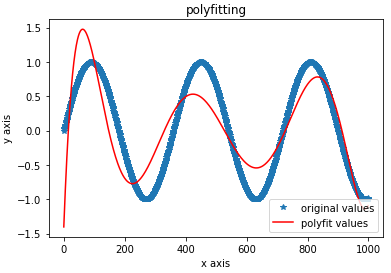
5. np.polyfit函数：采用的是最小二次拟合，numpy.polyfit(x, y, deg, rcond=None, full=False, w=None, cov=False)，前三个参数是必须的

官方文档：https://docs.scipy.org/doc/numpy-1.13.0/reference/generated/numpy.polyfit.html

6. np.polyld函数：得到多项式系数，主要有三个参数

    A one-dimensional polynomial class.

    A convenience class, used to encapsulate "natural" operations on
    polynomials so that said operations may take on their customary
    form in code (see Examples).

    Parameters
    ----------
    c_or_r : array_like
        The polynomial's coefficients, in decreasing powers, or if
        the value of the second parameter is True, the polynomial's
        roots (values where the polynomial evaluates to 0).  For example,
        ``poly1d([1, 2, 3])`` returns an object that represents
        :math:`x^2 + 2x + 3`, whereas ``poly1d([1, 2, 3], True)`` returns
        one that represents :math:`(x-1)(x-2)(x-3) = x^3 - 6x^2 + 11x -6`.
    r : bool, optional
        If True, `c_or_r` specifies the polynomial's roots; the default
        is False.
    variable : str, optional
        Changes the variable used when printing `p` from `x` to `variable`
        (see Examples).

参数1表示：在没有参数2（也就是参数2默认False时），参数1是一个数组形式，且表示从高到低的多项式系数项，例如参数1为[4,5,6]表示：

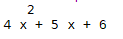
 参数2表示：为True时，表示将参数1中的参数作为根来形成多项式，即参数1为[4,5,6]时表示：(x-4)(x-5)(x-6)=0，也就是：

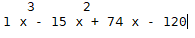
 参数3表示：换参数标识，用惯了x，可以用 t，s之类的

用法：

1. 直接进行运算，例如多项式的平方，分别得到

xx=np.poly1d([1,2,3])
print(xx)
yy=xx**2  #求平方，或者用 xx * xx
print(yy)

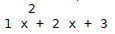
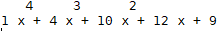
2. 求值：

yy(1) = 36

3. 求根：即等式为0时的未知数值

yy.r

4. 得到系数形成数组：

yy.c 为：array([ 1,  4, 10, 12,  9])

5. 返回最高次幂数：

yy.order = 4

6. 返回系数：

yy[0] —— 表示幂为0的系数

yy[1] —— 表示幂为1的系数

参考：

https://www.cnblogs.com/zhouzhe-blog/p/9621679.html