全局最小割StoerWagner算法详解

前言

StoerWagner算法是一个找出无向图全局最小割的算法，本文需要读者有一定的图论基础。

本文大部分内容与词汇来自参考文献（英文，需科学上网），用兴趣的可以去读一下文献。

---

概念

• 无向图的割：有无向图\(G=(V,E)\)，设\(C\)为图\(G\)中一些弧的集合，若从\(G\)中删去\(C\)中的所有弧能使图\(G\)不是连通图，称\(C\)图\(G\)的一个割。
• \(S-T\)割：使得顶点\(S\)与顶点\(T\)不再连通的割，称为\(S-T\)割
• \(S-T\)最小割：包含的弧的权和最小的\(S-T\)割，称为\(S-T\)最小割。
• 全局最小割：包含的弧的权和最小的割，称为全局最小割。
• 诱导割(induced cut)：令图\(G=(V, E)\)的一个割为\(C\)，则割\(C\)在图\(G\)的子图\(G'=(V',E')\)中的部分称为割\(C\)的诱导割。（类似于概念诱导子图(induced subgraph)）

---

算法流程

大致流程

step1：在图\(G\)中找出任意\(s-t\)最小割cut-of-the-phase

step2：合并\(s\)、\(t\)，重复执行step1直到图G只剩下一个顶点

step3：输出最小的cut-of-the-phase为最终结果

伪代码：

def MinimumCutPhase(G, w, a):
    A ← {a}
    while A ≠ V:
        把与A联系最紧密（most tightly）的顶点加入A中
    cut-of-the-phase ← w(A \ t, t)
    合并最后两个加入到A的顶点s、t
    return cut-of-the-phase

def StoerWagner(G, w, a):
    while |V| > 1
        MinimumCutPhase(G, w, a)
        根据返回值更新最小割

其中：

• \(w\)为边权函数，\(w(e)\)为边\(e\)的权值大小
• \(w(A, v)\)为顶点\(v\)到集合\(A\)的所有边权和
• \(x\)与\(A\)联系最紧密（most tightly）当且仅当\(x \notin A\)且\(w(A,x) = max\{w(A, y) | y \notin A\}\)
• \(a\)可以取任意顶点作为算法的初始顶点

---

证明

首先，算法基于这样一个事实：

两个顶点s、t，要么在全局最小割的同一个集合中，要么在不同的集合中

那么结果便只可能在是\(s-t\)最小割，或者合并\(s\)、\(t\)的新图的全局最小割。

然后问题就在于如何寻找任意的\(s-t\)最小割。现在来证明MinimumCutPhase找出来的\(s-t\)割cut-of-the-phase为什么是最小的。

定理：每个阶段割(cut-of-the-phase)是当前图的\(s-t\)最小割，\(s\)、\(t\)是当前阶段最后加入的结点。

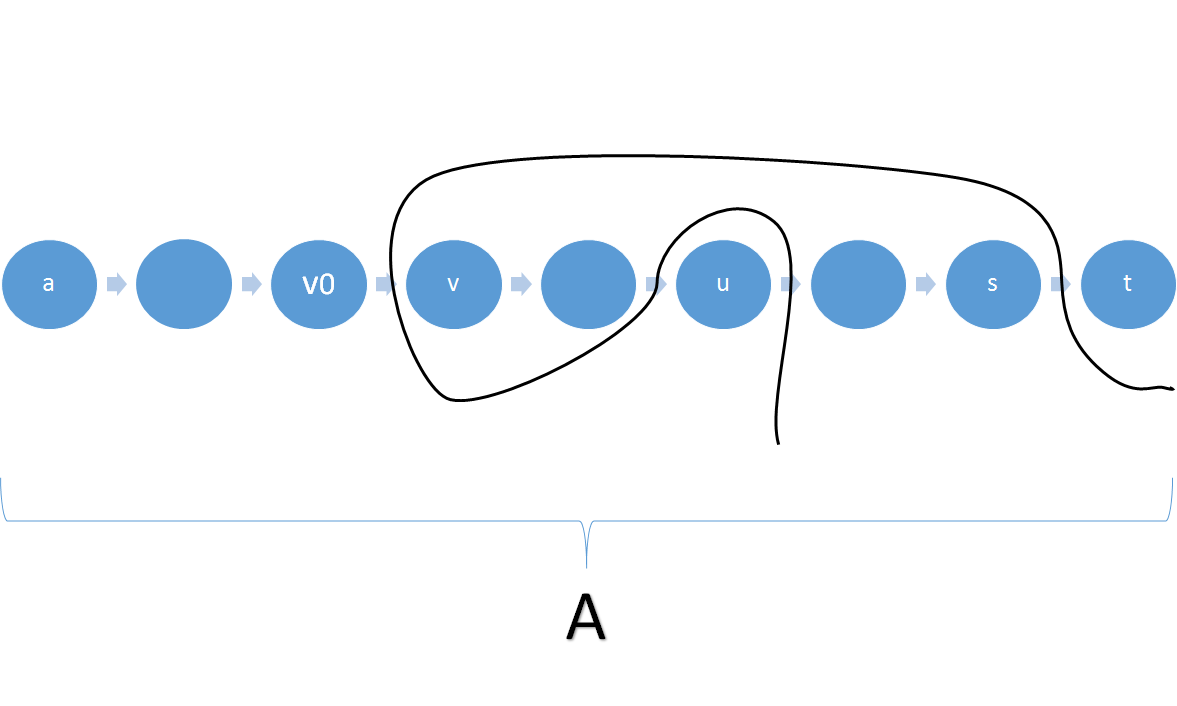
证明：

以加入集合\(A\)的顺序组成一个序列，以\(a\)为开始，以\(s\)、\(t\)结束。然后来证明对于任意\(s-t\)割\(C\)均不小于阶段割(cut-of-the-phase)

我们称结点\(v\)(\(v \neq a\))是活跃的(active)当\(v\)和\(v\)的前一个结点分立于C的两边。令\(w(C)\)为割C的大小，\(A_v\)为所有在\(v\)前面的顶点（不包括\(v\)），\(C_v\)为\(A_v \bigcup \{v\}\)的\(C\)割，\(w(C_v)\)为诱导割\(C_v\)的大小。

那么，对于所有活跃的顶点v，有

\[w(A_v,v) \leq w(C_v) \cdots \cdots (1)
\]

归纳证明:

对于第一个活跃顶点\(v_0\)，该不等式以等号成立。这是由于\(v_0\)前面的点都非活跃点，那么它们都在割C的同一侧，另一侧为\(v_0\)，显然有\(w(A_{v_0},v_0) = w(C_{v_0})\)。

假设对于活跃顶点\(v\)，\(v\)满足不等式。令\(u\)为\(v\)的下一个活跃顶点，那么我们令：

\[w(A_u,u)=w(A_v,u)+w(A_u \setminus A_v,u)=:\alpha
\]

由于\(v\)加入\(A\)比\(u\)早，所以有\(w(A_v,u) \leq w(A_v,v)\)。又因\(v\)满足不等式，所以有

\[w(A_v,u) \leq w(A_v,v) \leq w(C_v)
\]

由于所有 \(A_u \setminus A_v\) 与\(u\)之间的边均跨过割\(C_u\)，且不是\(C_v\)的一部分，于是有

\[w(C_v)+w(A_u \setminus A_v,u) \leq w(C_u)
\]

联立上式，得到：

\[\alpha \leq w(C_v)+w(A_u \setminus A_v,u) \leq w(C_u)
\]

于是对于任意活跃顶点，均满足不等式\((1)\)。

由于\(t\)总是活跃顶点（\(s-t\)割导致\(s\)与\(t\)总被割开），则\(t\)总是满足不等式\(w(A_t,t) \leq
w(C_t)\)，即任意割小于等于\(w(A_t,t)\)。又因为\(w(A_t,t)\)为单独割掉顶点\(t\)的大小（链接\(t\)的所有边权和），所以有\(w(A_t,t)\)为\(s-t\)最小割。证得MinimumCutPhase找出来的\(s-t\)割是\(s-t\)最小割。

---

例题

HDU 3691 Nubulsa Expo（全局最小割Stoer-Wagner算法）

HDU 6081 度度熊的王国战略（全局最小割Stoer-Wagner算法）

---

参考文献

stoerwagner-mincut.[Stoer-Wagner,Prim,连通性,无向图,最小边割集]