多校A层冲刺NOIP2024模拟赛20

昨天晚上打 ABC 了，所以今天才发。

T1 星际联邦

直接上菠萝（Borůvka）算法就行了，当然还可以用线段树优化 prim算法，但是没打过只是口胡：就是维护当前的连通块，但一个点 $ i $ 加入连通块时，后面那些点就可以有 $ a_j - a_i $ 的贡献，前面的点可以有 $ a_i - a_j $ 的贡献，然后区间修改，同时自己不可以再被选，单点修改自己为 inf ，然后全局查询即可。

QED 赛时发明了一种 $ o(n) $ 做法，经证明是正确的，不会，run了。

T2 和平精英

\[越 \ \& \ 越小，越 \ | \ 越大。
\]

赛时能想到按值域去枚举，是 $ O(qn^2) $ 的，因为从值域上去枚举最后两者的答案是 $ v $ 的话， $ \gt v $ 的只能给 & ， $ \lt v $ 的只能给 | ， $ = v $ 的需要分讨一下：如果超过两个的话那就两边各一个，如果只有一个的话，那就分别给两边看看哪种可以。

然后其中一个 $ n $ 是因为我们要枚举求那些数 & 的和，和 | 的和，但是这可以直接用线段树优化到 $ log(n) $ ，于是有了 $ O(qnlog(n)) $ 的做法。

我们之所以枚举值域是因为他在值上满足越 & 越小，越 | 越大。其实这个性质在 popcount 上也满足，所以我们直接枚举 popcount 是 v ，但是这个时候 $ = v $ 的情况又有点麻烦，因为我不确定他的值到底是多少，但是你发现如果他们的值不同的话，不管给谁他们最后的值一定不相同，所以特判相同之后继续上面的分讨即可。还有一个就是两个党派必须都有人，这也有点麻烦，但是就是多点细节的事。时间复杂度 $ o(nlog^2(n)) $

T3 摆烂合唱

每相邻的两个数进行一次运算之后会合并成一个数，那么让合并之后的这个数是原来两个数的 fa，然后最后一定会合并成一个数，对于最后这个数我们直到他的答案，然后我们树上DP就行。

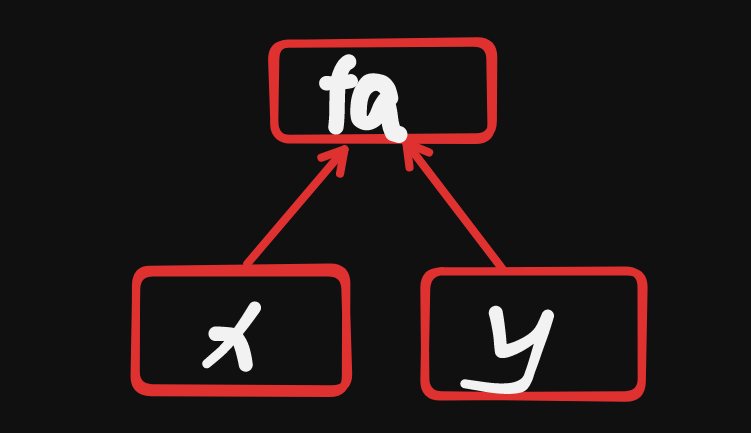
如果我们此时知道了 $ fa $ 的所有信息，那我们如何得知 $ x $ 的答案？

先假设 $ y = 1 $

如果 $ x $ 不管选什么 $ fa $ 都 = 1/0 的话，那么 $ x $ 选择不同导致最后答案不同的概率就会加上 $ fa $ 是 1/0 时最终答案不同的概率 $ \times $ y = 1 的概率。否则就会加上 $ fa $ 不同时的概率 $ \times $ y=1 的概率。

那么其他情况同理，我们只需要维护 $ ans_0 $ 表示 $ x $ 为 0 时答案不同的概率， $ ans_1 $ 表示 $ x $ 为 1 时答案不同的概率， $ ans_2 $ 表示 $ x $ 不同时答案不同的概率（也是最后要求的答案），然后从下到上算一个数为 0/1 的概率，再从上到下DP算答案即可。

T4 对称旅行者

这个题解讲的其实挺清楚的，所以以解释题解为主：

题解：

考虑先求旅行者 $i$ 的期望位置，设为 $f_i$，那么答案就为 $f_i * 2^{m K}$。

当旅行者 $i$ 旅行时时，由于期望的线性性，$f_i \longleftarrow \frac{1}{2}\left(2 f_{i-1}-f_i+2 f_{i+1}-f_i\right)=f_{i-1}+f_{i+1}-f_i$，考虑其几何含义，发现是把 $f_i$ 关于 $f_{i-1}$ 和 $f_{i+1}$ 的中点对称，如果设 $g_i=f_{i+1}-f_i$，那么跳第 $i$ 枚棋子相当于交换 $g_{i-1}$ 和 $g_i$。

因此一轮旅行就对应一个 $1 \sim n-1$ 的置换，用类似快速幂的方法就可以求出 $K$ 轮旅行后的 $\left\{g_i\right\}$，再注意到 $f_1$ 始终不变，就可以求出所有棋子的期望位置，时间复杂度为 $O(n \log K)$。

[==============]

首先 $ x $ 关于 $ y $ 对称后的位置可以写成 $ y*2-x $ ，所以第一个式子很好理解，然后就是后面的几何意义，我们把 $ f_{i-1} + f_{i+1} $ 看成 $ \frac{ f_{i-1} + f_{i+1} }{2} \times 2 $ ，所以这和对称的那个式子一样，然后就可以知道题解说的关于 $ f_{i-1} $ 和 $ f_{i+1} $ 的中点对称。

然后感性认为那个 $ g $ 就是正的，所以 $ g_i $ 表示 $ i $ 和 $ i+1 $ 之间的距离，所以 $ i $ 关于 $ i-1 , i+1 $ 中点对称时，就是交换了两者之间的距离，然后再感性理解一下 $ g $ 是负的也成立。

所以成了置换环，快速幂即可求出最后的 $ g $ 数组，然后从数据范围中得知 $ f_1 $ 不变，所以可以算出最后的 $ f $ 数组，然后 $ ans_i = f_i \times 2^{km} $ 。